有问题的球

题目描述

有12个外观一致的小球，其中有一个是残次品，重量和其他的小球不一致，借助一个没有刻度的天平，最少测量几次可以找出有问题的小球？

思路解析

把12个球分成3组，分别为A组、B组、C组，小球的初始分布如下图，小球颜色只是为了更好理解，不同的颜色也可以放在同一组。

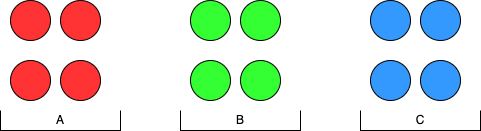
定义weight(X)表示X的重量。

A组和B组进行称重比较，存在三种情况（A组较重，B组较重，两组一样重），但是weight(A) < weight(B)和weight(A) > weight(B)这两种情况是对称的，只需要把A组和B组中所有的球交换就变成同一种情况，所以下面我们只讨论weight(A) < weight(B)和 weight(A) == weight(B)两种情况。

小球分成三组是因为利用天平一次就可以确定出三组中有问题的组；分成两组的效率就比较低因为log₂12 > log₃12，要比较更多次；分成更多组就无法一次确定有问题的组。

如果 weight(A) < weight(B)

此时可以得到两个有用信息：

• A组中有一个较轻的球或者B组中有一个较重的球。

• C组中的球是没问题的。

从C组中拿出3个球替换A组中的3个球，用A组中替换下来的3个球替换B组中的3个球，此时小球的分布如下图所示。

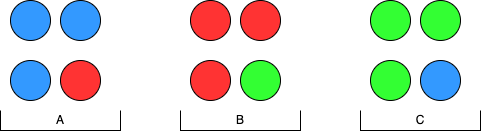
1. 如果替换后 weight(A) < weight(B)，天平和之前保持一致，说明有问题的球位置没有变动。此时要么A组未被替换的球比较轻，要么B组中未被替换的球比较重，这个时候只需要把A组中未被替换的球跟任意一个正常的球比较，如果相等，则B组中未被替换的球为次品且相比其他球较重。否则A组中未被替换的球为次品且相比其他球较轻。

2. 如果替换后 weight(A) == weight(B)，说明此时A组和B组中都是好球，只有B组被替换走的3个球离开了天平，说明它们是问题的，用天平称一下其中的两个球就能找到有问题的那个球，且可以知道这个有问题的球相比其他球较重。

3. 如果替换后 weight(A) > weight(B)，说明较轻的球从A组移到了B组，用天平称一下从A组移到B组的三个球中的两个就能找到有问题的那个球，且可以知道有问题的球相比其他球较轻。

这里小球三三互换也是因为天平一次性最多能区分三个小球中的坏球，你也可以尝试一下一一互换，两两互换都是需要更多称量次数的。

如果 weight(A) == weight(B)

此时有问题的球在C组中。

从A组和C组各拿出三个球比较，如下图。

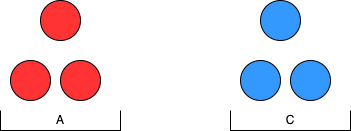
1. 如果 weight(A) == weight(C)，说明C组中剩下的那个球有问题，只需要再和其他球比较一次即可判断是轻还是重。

2. 如果 weight(A) < weight(C)， 说明C组中存在一个较重的球，只要再从C组中参与称重的3个球中拿出两个再称一次就可以确定较重的那一个球。

3. 如果 weight(A) > weight(C)，说明C组中存在一个较轻的球，只要再从C组中参与称重的3个球中拿出两个再称一次就可以确定较轻的那一个球。

综上讨论，至少需要3次区分出有问题的小球，并确定小球是重还是轻。