题目链接： https://leetcode.cn/problems/word-search/

LeetCode 79. 单词搜索

题目描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

举个例子：

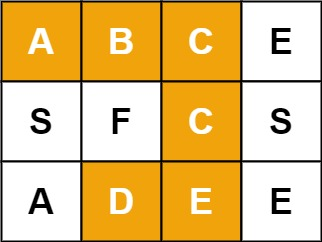
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

知识回顾

深度优先搜索（Depth-First Search，DFS）是一种常见的图遍历算法，它从图的某个顶点开始遍历，沿着一条路径一直走到底，直到不能再走为止，然后回溯到前一个节点，继续沿着另一条路径走到底，直到所有的节点都被访问过为止。

在实现深度优先搜索时，可以使用递归或栈来保存遍历的路径。具体来说，从起始节点开始，将其标记为已访问，然后遍历与该节点相邻的未访问节点，对于每个未访问节点，递归调用深度优先搜索函数，直到所有与起始节点相连的节点都被访问过为止。

思路解析

本题的思路比较清晰，采用深度优先搜索，深搜一般采用递归来实现，本题的关键就是确定递归的结束条件。

从二维数组的四周边界元素开始dfs搜索，搜索到目标单词就返回true，否则，所有的路径都搜索完也没搜到目标单词就返回false。

假设二维数组board = [['F', 'C', 'S'], ['F', 'E', 'D'], ['A', 'B', 'C']]。

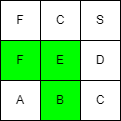
要搜索的字符串word = "BEF"，那么从board边界坐标(2, 1)即字符B开始，按照下右上左的顺序进行dfs的过程如下图，因为每个字符最多有四个相邻字符，所以搜索树是一个四叉树。

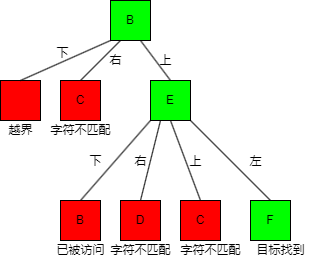
从字符B搜索到字符C发现不匹配，把字符C置为未被访问的状态，回溯到字符B，接着对字符E进行搜索，直到搜索到字符F，整个word被搜索到，返回true。

定义变量i为递归的深度，也表示word的第i个字符，row为二维数组board的行，col为二维数组board的列。

递归结束的条件如下：

1. 递归深度i == word.length()，说明在board中搜索到了word，结束搜索返回true。
2. 递归深度i < word.length()，如果坐标(row, col)在board边界之外 或 board[row][col] != word[i] 或 坐标(row, col)已被访问过 就结束搜索返回false，否则继续向四周搜索。

C++代码

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        int rows = board.size();
        int cols = board[0].size();
        vector<vector<bool>> visit(rows, vector<bool>(cols, false));
        for (int row = 0; row < rows; ++row) {
            for (int col = 0; col < cols; ++col ) {
                if (dfs(row, col, 0, board, word, visit)) {
                    return true;
                }
            }
        }
        return false;
    }
    //row：board的行，col：board的列，i：递归的深度也是word的第i个字符，visit：保存board中元素是否访问过
    bool dfs(int row, int col, int i, vector<vector<char>>& board, string& word, vector<vector<bool>>& visit) {
        if (i == word.length()) {
            return true;
        }
        int rows = board.size();
        int cols = board[0].size();
        if (row >= rows || row < 0 || col >= cols || col < 0 || board[row][col] != word[i] || visit[row][col]) {
            return false;
        }

        visit[row][col] = true;
        bool res = false;
        //向下搜索
        res |= dfs(row + 1, col, i + 1, board, word, visit);
        //向右搜索
        res |= dfs(row, col + 1, i + 1, board, word, visit);
        //向上搜索
        res |= dfs(row - 1, col, i + 1, board, word, visit);
        //向左搜索
        res |= dfs(row, col - 1, i + 1, board, word, visit);
        visit[row][col] = false;

        return res;
    }
};

复杂度分析

时间复杂度： board中的每一个元素都要进行深度优先搜索，这里的深搜使用递归来实现的，这里的递归展开来是一个高度为k的四叉树，所以时间复杂度为O(mn4^k)，其中m是board的行数，n是board的列数。

空间复杂度： 借用了一个visit数组和递归调用栈，所以空间复杂度为O(mn)，递归调用栈和word的长度有关，一般不会比mn长。其中m是visit的行数，n是visit的列数。