题目链接： https://leetcode.cn/problems/pacific-atlantic-water-flow/

LeetCode 417.太平洋大西洋水流问题

题目描述

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

举个例子：

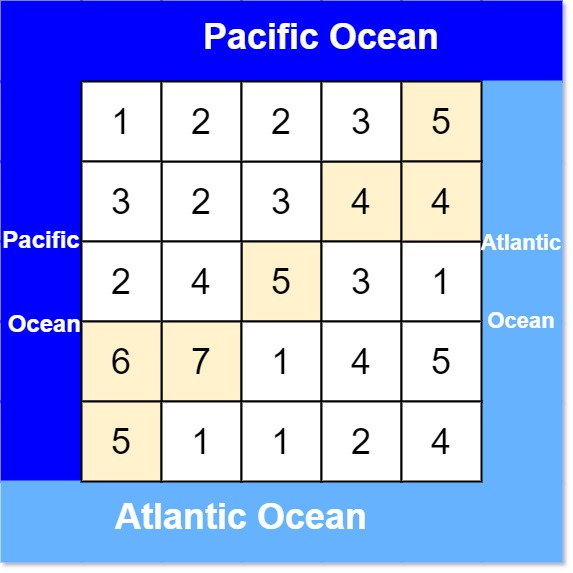
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

知识回顾

深度优先搜索（Depth-First Search，DFS）是一种常见的图遍历算法，它从图的某个顶点开始遍历，沿着一条路径一直走到底，直到不能再走为止，然后回溯到前一个节点，继续沿着另一条路径走到底，直到所有的节点都被访问过为止。

在实现深度优先搜索时，可以使用递归或栈来保存遍历的路径。具体来说，从起始节点开始，将其标记为已访问，然后遍历与该节点相邻的未访问节点，对于每个未访问节点，递归调用深度优先搜索函数，直到所有与起始节点相连的节点都被访问过为止。

思路解析

首先明确本题的目标：求水流既可以流向太平洋也可以流向大西洋的坐标的集合。 下图中的坐标(2,2)就是一个满足条件的坐标。

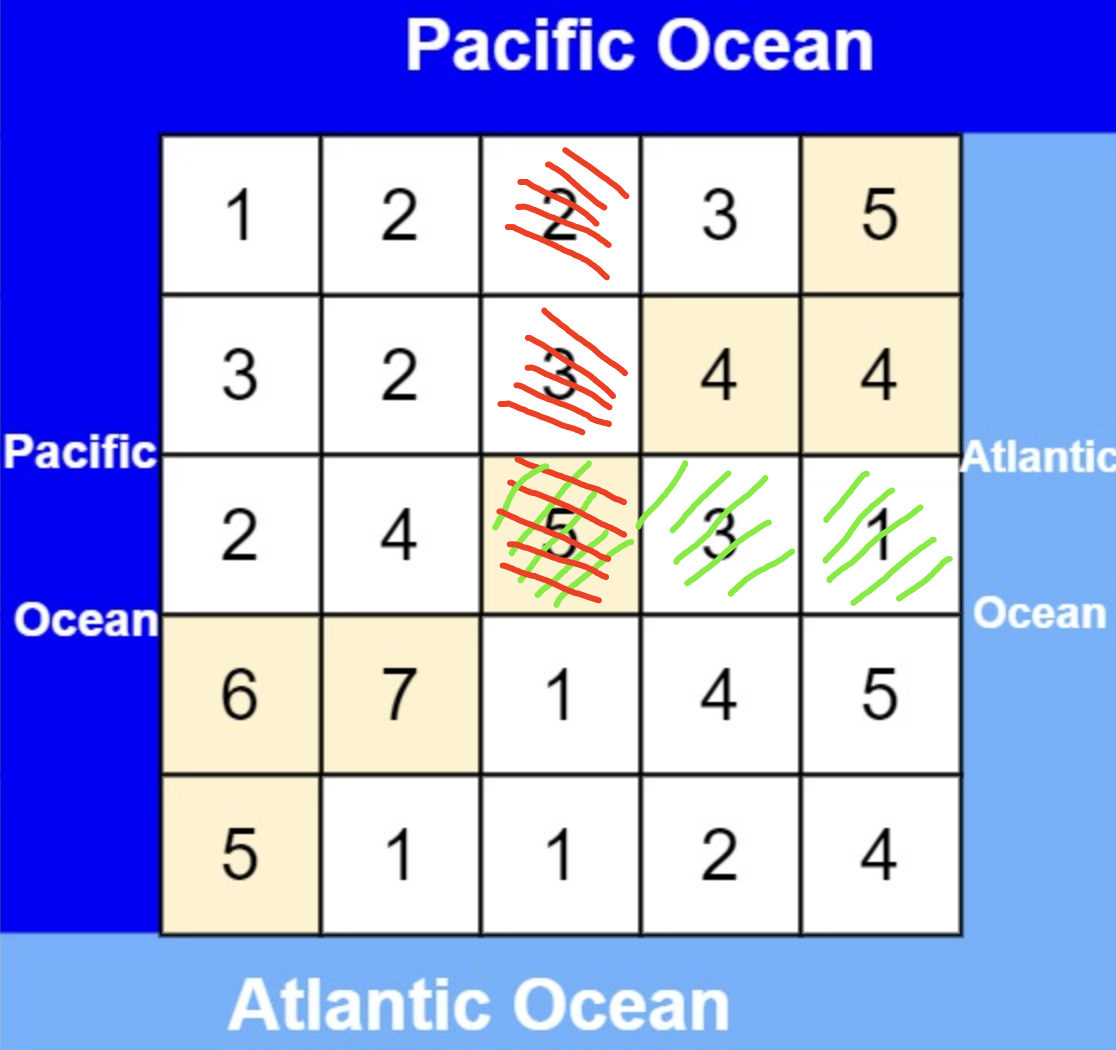
本题可以使用 深度优先搜索(DFS) 来解。使用两个数组pac_visit保存坐标(i,j)的水是否可以流向太平洋，atl_visit保存坐标(i,j)的水是否可以流向大西洋。

算法如下：

1. 对所有毗邻太平洋的坐标点进行dfs，确定所有能流向太平洋的坐标点并保存到pac_visit。
2. 对所有毗邻大西洋的坐标点进行dfs，确定所有能流向大西洋的坐标点并保存到atl_visit。
3. 遍历数组pac_visit和atl_visit，把既可以流向太平洋又可以流向大西洋的坐标保存到数组res，并返回。

这里的深搜(dfs)是使用递归实现的，结束的条件是当前坐标超出矩阵范围或当前坐标对应的高度小于上一个坐标对应的高度（保证水往低处流）或当前坐标已经被标记过。

C++代码

class Solution {
public:
    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
        //保存结果
        vector<vector<int>> res;
        int rows_cnt = heights.size();
        int cols_cnt = heights[0].size();
        //能流向太平洋的坐标
        vector<vector<bool>> pac_visit(rows_cnt, vector<bool>(cols_cnt, false));
        //能流向大西洋的坐标
        vector<vector<bool>> atl_visit(rows_cnt, vector<bool>(cols_cnt, false));
        for (int i = 0; i < cols_cnt; ++i) {
            //对矩阵的上边每个毗邻太平洋的坐标进行dfs
            dfs(heights, 0, i, pac_visit, heights[0][i]);
            //对矩阵下边每个毗邻大西洋的坐标进行dfs
            dfs(heights, rows_cnt - 1, i, atl_visit, heights[rows_cnt - 1][i]);
        }

        for (int i = 0; i < rows_cnt; ++i) {
            //对矩阵左边每个毗邻太平洋的坐标进行dfs
            dfs(heights, i, 0, pac_visit, heights[i][0]);
            对矩阵右边每个毗邻大西洋的坐标进行dfs
            dfs(heights, i, cols_cnt - 1, atl_visit, heights[i][cols_cnt - 1]);
        }

        for (int i = 0; i < rows_cnt; ++i) {
            for (int j = 0; j< cols_cnt; ++j) {
                if (pac_visit[i][j] && atl_visit[i][j]) {
                    //保存既可以流向大西洋又可以流向太平洋的坐标点
                    res.push_back({i,j});
                }
            }
        }

        return res;
    }

    void dfs(vector<vector<int>>& heights, int row, int col, vector<vector<bool>>& visit, int prevHeight) {
        //递归的返回条件，当前坐标超出矩阵范围 或 当前坐标对应的高度小于上一个坐标对应的高度 或 当前坐标已经被标记过
        if (row < 0 || col < 0 || row == heights.size() || col == heights[0].size() || heights[row][col] < prevHeight || visit[row][col]) {
            return;
        }
        visit[row][col] = true;
        //对当前坐标的右边坐标进行dfs
        dfs(heights, row + 1, col, visit, heights[row][col]);
        //对当前坐标的左边坐标进行dfs
        dfs(heights, row - 1, col, visit, heights[row][col]);
        //对当前坐标的下面坐标进行dfs
        dfs(heights, row, col + 1, visit, heights[row][col]);
        //对当前坐标的上面坐标进行dfs
        dfs(heights, row, col - 1, visit, heights[row][col]);
    }
};

复杂度分析

时间复杂度： O(n)， n为坐标的总数。

空间复杂度： O(n)， n为坐标的总数。