 接雨水
接雨水
题目链接: https://leetcode.cn/problems/trapping-rain-water/
# LeetCode 42. 接雨水
# 题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
举个例子

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
# 思路解析
采用逐列计算,计算每列最多能接雨水量,然后把每列能接的雨水量加起来,就可以得到所有柱子总的接雨水量。
那么对于第i列,要怎样计算它能接的雨水量呢?
我们可以找出0 ~ i列最高的柱子,记为maxL,然后找到i ~ n列最高的柱子,记为maxR,maxL和maxR分别是第i列的左右边界,因为第i列能接的雨水量是由较短的那个边界决定的,所以min(maxL, maxR) - height[i]就是第i列能接的雨水量,下图中的红色区域就是第i列可以接的雨水量。
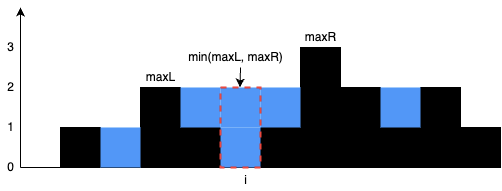
我们以上面的数组height = [0,1,0,2,1,0,1,3,2,1,2,1]为例,来看一下整个接雨水的过程。
- 从左到右遍历数组,来计算
0 ~ i列最高的柱子maxL,即第i列的左边界。
| height | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 3 | 2 | 1 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| maxL | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
- 从右到左遍历数组, 来计算
n ~ i列最高的柱子maxR,即第i列的右边界。。
| height | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 3 | 2 | 1 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| maxL | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
| maxR | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 1 |
- 计算
min(maxL, maxR),即较短的边界长度。
| height | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 3 | 2 | 1 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| maxL | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
| maxR | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 1 |
| min(maxL, maxR) | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 2 | 2 | 2 | 1 |
- 计算每一列能接的雨水量
min(maxL, maxR) - height[i],即较短的边界减去第i列柱子本身的高度。
| height | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 3 | 2 | 1 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| maxL | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
| maxR | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 1 |
| min(maxL, maxR) | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 2 | 2 | 2 | 1 |
| min(maxL, maxR)-height[i] | 0 | 0 | 1 | 0 | 1 | 2 | 1 | 0 | 0 | 1 | 0 | 0 |
- 把所有的
min(maxL, maxR)-height[i]>0的值加在一起就是能接雨水的总量。
上面的整个过程需要借助额外的空间,空间复杂度为O(n),其中n为数组中元素的个数。
我们可以使用双指针法对上面的步骤进行优化。
定义L指向数组的第一个元素,R指向数组的最后一个元素,初始化左右边界maxL = height[L], maxR = height[R]。
因为每一列接到雨水的量是由较短的边界决定的,所以一旦某一列左右边界的较短边界确定了,我们就可以计算对应列可接的雨水量,每次计算左右边界maxL和maxR中较小值对应的列就可以达到这个目的。
如果
maxL < maxR,此时L对应列的较短边界是确定的,利用公式maxL - height[L]计算L对应列可以接到雨水的量,大于0就累加到结果中,并将L向右移动一步++L,更新maxL = max(maxL, height[L])。如果
maxL >= maxR,此时R对应列的较短边界是确定的,利用公式maxR - height[R]计算R对应列可以接到雨水的量,大于0就累加到结果中,并将R向左移动一步--R,更新maxR = max(maxR, height[R])。
# c++代码
class Solution {
public:
int trap(vector<int>& height) {
int res = 0;
//定义两个指针
int left = 0, right = height.size() - 1;
//定义待计算列的左右边界
int maxL = height[left], maxR = height[right];
while (left <= right) {
//计算较小边界对应指针指向的列接雨水的量
if (maxL < maxR) {
int temp = maxL - height[left];
if (temp > 0)
res += temp;
++left;
//防止越界访问
if (left < height.size())
maxL = max(maxL, height[left]);
} else {
int temp = maxR - height[right];
if (temp > 0)
res += temp;
--right;
//防止越界访问
if (right >= 0)
maxR = max(maxR, height[right]);
}
}
return res;
}
};
# java代码
class Solution {
public int trap(int[] height) {
int res = 0;
//定义两个指针
int left = 0, right = height.length - 1;
//定义待计算列的左右边界
int maxL = height[left], maxR = height[right];
while (left <= right) {
//计算较小边界对应指针指向的列接雨水的量
if (maxL < maxR) {
int temp = maxL - height[left];
if (temp > 0) {
res += temp;
}
left++;
//防止越界访问
if (left < height.length) {
maxL = Math.max(maxL, height[left]);
}
} else {
int temp = maxR - height[right];
if (temp > 0) {
res += temp;
}
right--;
//防止越界访问
if (right >= 0) {
maxR = Math.max(maxR, height[right]);
}
}
}
return res;
}
}
# python代码
class Solution:
def trap(self, height: List[int]) -> int:
res = 0
#定义两个指针
left, right = 0, len(height) - 1
#定义待计算列的左右边界
maxL, maxR = height[left], height[right]
while left <= right:
#计算较小边界对应指针指向的列接雨水的量
if maxL < maxR:
temp = maxL - height[left]
if temp > 0:
res += temp
left += 1
#防止越界访问
if left < len(height):
maxL = max(maxL, height[left])
else:
temp = maxR - height[right]
if temp > 0:
res += temp
right -= 1
#防止越界访问
if right >= 0:
maxR = max(maxR, height[right])
return res
# 复杂度分析
时间复杂度: 只需要遍历一遍数组,所以时间复杂度为O(n),其中n为数组的大小。
空间复杂度: 只用到两个指针,所以空间复杂度为O(1)。
