如何理解递归

递归是一种把问题分解成独立子问题来求解的编程方法，一个问题要使用递归来解决需要确定下面两个关键点：

1. 确定独立子问题的划分。
2. 确定递归的返回条件。

如果上面两点没有明确就开始撸代码，可能会导致无限递归下去，很容易把程序的栈给打爆。

下面通过一个简单的例子斐波那契数列带大家看一下递归的过程。

斐波那契数列的定义如下：

fib(0) = 0
fib(1) = 1
fib(n) = fib(n - 1) + fib(n - 2), n >= 2

求解fib(4)的c++代码如下，为了更容易理解，我在函数的入口，出口以及递归返回的条件都加了打印。

#include <iostream>
#include <iomanip>

int fib(int n) {
    std::cout << std::setw((4-n)*4)<< " " << "开始计算fib(" << n <<")\n" << std::endl;
    if (n == 0) {
        std::cout<< std::setw((4-n)*4) << " " << "n == 0,返回0\n" << std::endl;
        return 0;
    }

    if (n == 1) {
        std::cout<< std::setw((4-n)*4) << " " << "n == 1,返回1\n" << std::endl;
        return 1;
    }

    int res = fib(n - 1) + fib(n - 2);
    std::cout << std::setw((4-n)*4)<< " " << "计算fib(" << n <<")结束\n" << std::endl;
    return res;
}

int main()
{
    int n = 4;
    int res = fib(n);
    std::cout << " f(" << n << ") = " << res << "\n" << std::endl;
    return 0;
}

编译运行，输出如下：

开始计算fib(4)

    开始计算fib(3)

        开始计算fib(2)

            开始计算fib(1)

            n == 1,返回1

                开始计算fib(0)

                n == 0,返回0

        计算fib(2)结束

            开始计算fib(1)

            n == 1,返回1

    计算fib(3)结束

        开始计算fib(2)

            开始计算fib(1)

            n == 1,返回1

                开始计算fib(0)

                n == 0,返回0

        计算fib(2)结束

 计算fib(4)结束

 f(4) = 3

整个运行过程相当于对下面这棵树进行深度优先搜索。

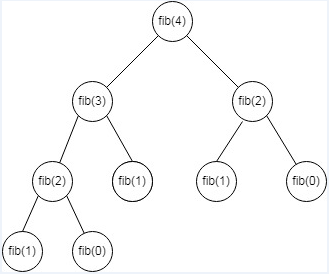
用gdb对编译出来的二进制进行调试，在返回条件if (n == 1)代码分支中加入断点，运行二进制，等程序断下来后，执行命令bt查看函数调用栈。

(gdb) bt
#0  fib (n=1) at test.cpp:12
#1  0x0000000000400a2b in fib (n=2) at test.cpp:16
#2  0x0000000000400a2b in fib (n=3) at test.cpp:16
#3  0x0000000000400a2b in fib (n=4) at test.cpp:16
#4  0x0000000000400ac4 in main () at test.cpp:24

可以看出来函数的调用顺序和我们上面日志中输出的顺序是一致的。

我们常说递归是通过栈来实现的，就是因为递归中会用到栈来保存函数的调用顺序。

上面对斐波那契数列的递归实现不是最优的，通过打印我们可以看到fib(2)被计算了多次，其实可以将fib(2)的结果在第一次计算完就保存下来，后面可以直接使用，提高程序的运行效率，这就是我们常说的空间换时间。这种实现方法也叫做备忘录法，刷题的时候是比较常见的。

上面的例子比较简单，目的是帮助大家更好理解递归，平时还需要多动手实践才能对递归有更深刻的理解。