 kmp算法详解
kmp算法详解
# kmp算法详解
kmp算法加快了字符串的匹配速度但也比较难理解,废话不多说,本文将带你深入理解一下kmp算法。
kmp算法匹配的过程中主串的索引在匹配失败时是不会回退的,只有模式串的索引根据next数组进行回退。暴力字符串匹配主串和模式串的索引在匹配失败时都会回退。相比之下,kmp算法的匹配速度能快很多。
# 1.前缀和后缀
首先要弄清什么是前缀和后缀,这是理解kmp算法的关键。
前缀是对于一个长为len的字符串,索引区间在[0,i]上的子串,其中 len-1 > i >= 0。
后缀是对于一个长为len的字符串,索引区间在[j,len-1]上的子串,其中 len > j > 0。
比如,字符串ldtech,其所有前缀下图:
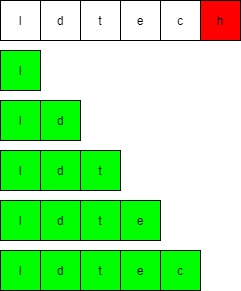
其所有后缀如下图:
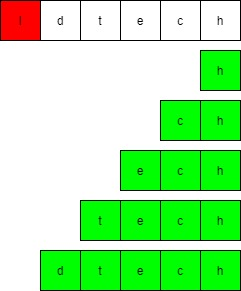
# 2.next数组的含义
next数组又叫前缀表,kmp算法的关键就是构造next数组,next数组到底是什么呢?
举个例子,主串str为:ababadabcee,模式串pat为:abadabce。
next[i]就是模式串pat在[0,i]区间上相同前后缀的最大长度。这句话看起来比较抽象,但是一定要多看几遍理解透。我特意画了张图来帮助大家来理解,结合这张图也许你就能豁然开朗。
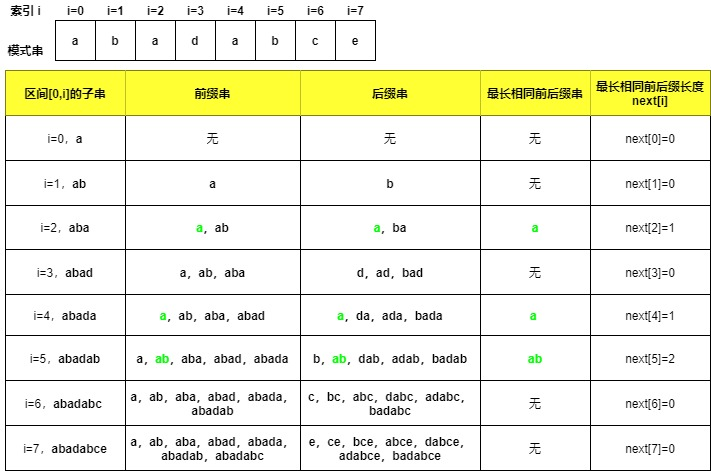
这些最长相同前后缀的长度就组成了next数组,next[i]实际上就是[0,i]区间上一个符合条件的前缀长度,这也是next数组称为前缀表的原因。
# 3.构造next数组
next数组的构造过程,实际上就是模式串的最长后缀作为主串,最长前缀作为模式串进行字符串匹配的一个过程。又是抽象的的一句话,别着急,慢慢往下看。
比如主串str为:ababadabcee,模式串pat为:abadabce,那么我们要得到next数组只需要将模式串pat的最长后缀badabce作为主串,最长前缀abadabc作为模式串进行匹配。
假设i,j均为模式串pat的索引,i遍历最长后缀,故i的范围为[1,7],j遍历最长前缀,故j的范围为[0,6],pat的长度为8。
匹配过程如下:
- 初始化
i=1,j=0,next[0]=0。 - 比较
pat[i]和pat[j],如果pat[i]==pat[j],进入步骤3。如果pat[i]!=pat[j],进入步骤4。 next[i]=j+1,++i,++j,i小于模式串pat的长度就进入步骤2。否则就结束。- 如果
j==0,那么next[i]=0,++i,i小于模式串pat的长度就进入步骤2。 否则j=next[j-1],进入步骤2。
下图展示了完整的匹配流程:
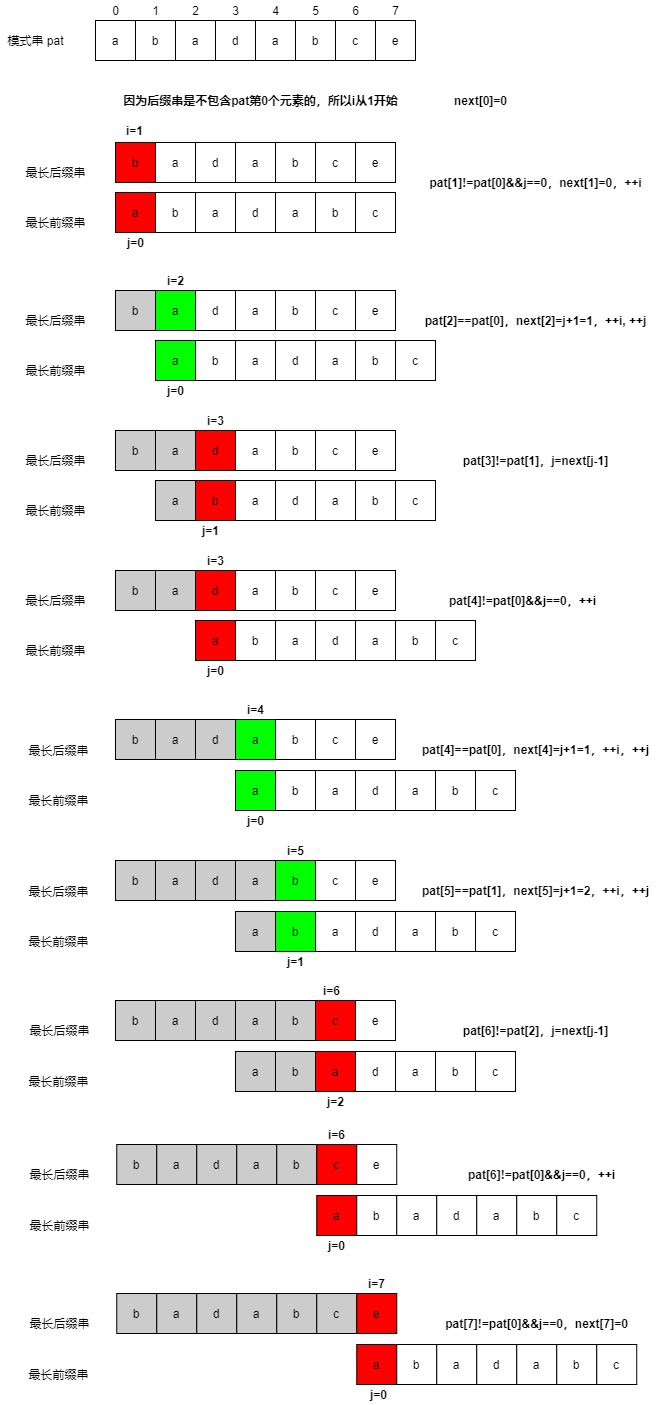
整个匹配的过程i是不回头的,j是根据next数组进行回退。
pat[i]==pat[j]时,next[i]=j+1是啥意思呢?pat[i]==pat[j]说明pat区间[0,j]和pat区间[i-j,i]是匹配的,可以保证他们是[0,i]区间的最长相同前后缀。此时前缀串长度为j+1,那么前缀表next[i]=j+1。如下图可以算出next[5]=2。
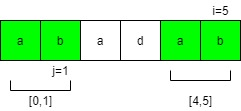
pat[i]!=pat[j]时,为啥j=next[j-1]呢?pat[i]!=pat[j],前面的匹配过程已经存储了next[j-1]的信息,只需将j进行回退到区间[0,j-1]的前缀的下一个位置next[j-1]继续匹配即可。如下图:
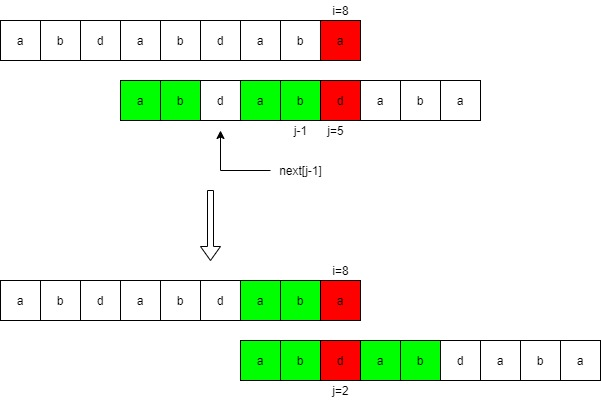
代码如下:
void create_next(string pat, vector<int>& next) {
int len = pat.length();
next[0] = 0;
int i = 1, j = 0;
while(i < len) {
if (pat[i] == pat[j]) {
//把前缀串的长度赋给next[i]
next[i] = j + 1;
++i;
++j;
} else {
//匹配失败且前缀串的长度为0
if (j == 0) {
next[i] = 0;
++i;
} else {
//匹配失败跳到前缀串的下一个元素继续匹配
j = next[j-1];
}
}
}
}
根据上面的步骤,我们就根据模式串pat得到了next数组。接下来就根据next数组来进行主串和模式串的匹配。
# 4.主串和模式串匹配
还是沿用了上面的例子主串str为:ababadabcee,模式串pat为:abadabce。
假设i为主串的索引,j为模式串的索引,i的范围为[0,10],j的范围为[0,7] 。
匹配过程如下:
- 初始化
i=1,j=0,next[0]=0。 - 比较
str[i]和pat[j],如果str[i]==pat[j],进入步骤3。如果str[i]!=pat[j],进入步骤4。 ++i,++j,i小于主串长度且j小于模式串长度就进入步骤2。否则就匹配成功。- 如果
j==0,那么next[i]=0,++i,i小于主串长度就进入步骤2。 否则j=next[j-1],进入步骤2。
匹配过程如下图:
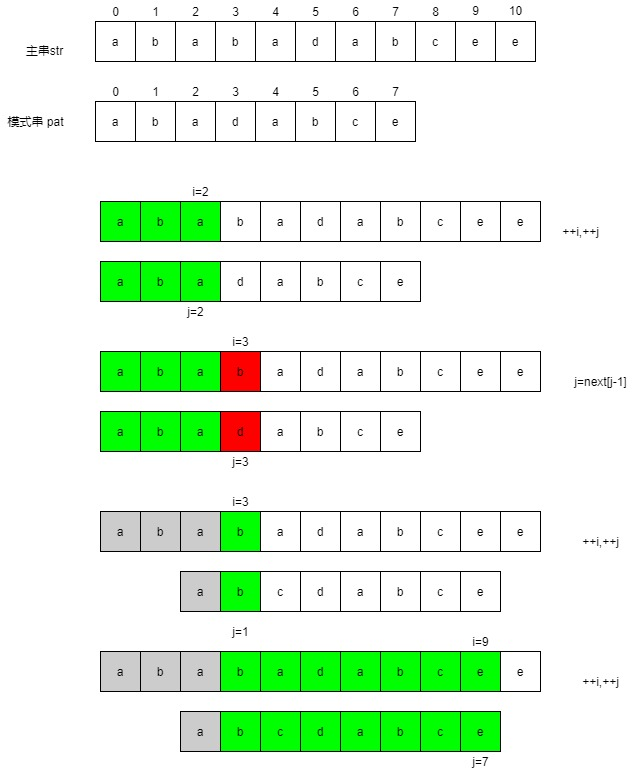
整个匹配的过程和next数组生成的过程非常相似,i是不回头的,j是根据next数组进行回退。理解了next数组的生成过程,就很容易理解主串和模式串的匹配过程。
代码如下:
int strStr(string str, string pat) {
int str_len = str.length();
int pat_len = pat.length();
vector<int> next(pat_len, 0);
create_next(pat, next);
int i = 0, j = 0;
while (i < str_len) {
if (str[i] == pat[j]) {
++i;
++j;
if (j == str_len) {
return i - j;
}
} else {
//匹配失败且前缀串的长度为0
if (j == 0) {
++i;
} else {
//匹配失败跳到前缀串的下一个元素继续匹配
j = next[j-1];
}
}
}
return -1;
}
输入主串str和模式串pat,strStr返回pat在str中的起始索引值。
# 5.复杂度分析
时间复杂度: 生成next数组需要遍历一遍模式串,主串和模式串匹配需要遍历一遍主串,故时间复杂度为O(m+n),其中m为主串长度,n为模式串长度。
空间复杂度: 生成next数组需要一个长为n的数组,主串和模式串匹配只需要两个索引,故空间复杂度为O(n),其中n为模式串长度。
