题目链接： https://leetcode.cn/problems/number-of-islands/

LeetCode 200.岛屿的数量

题目描述

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

举个例子：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

知识回顾

广度优先搜索（BFS） 是一种图形搜索算法，它的基本思想是从一个顶点出发，先访问它的所有邻接顶点，然后再按照同样的方式访问这些邻接顶点的未访问邻接顶点，直到图中所有顶点都被访问。广度优先搜索算法通常使用队列来存储待访问的顶点，并使用一个数组或者集合来记录已访问的顶点。

思路解析

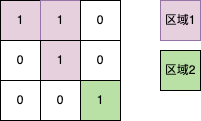
先明确怎样才能连成一个岛，水平方向或竖直方向的陆地(‘1’)相连，这样的陆地组成一个岛。如下图区域1和区域2属于不同的两个岛。

本题采用广度优先搜索来解，算法如下：

1. 采用数组visit来保存grid中的坐标是否被访问过。nums来保存岛屿的数量。
2. 对grid中所有未被访问过且grid[i][j] == 1的坐标(i, j)进行广搜并计数，++nums，每次搜索都能保证坐标所在的岛屿被遍历一遍。
3. 返回nums。

广搜都是采用队列来实现的，实现广搜的关键是明确入队的条件，本题的入队条件是根据当前坐标遍历其上下左右四个新坐标，新坐标没有被访问过，而且落在grid中，对应的值为1就把新坐标压入队列。

C++代码

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int nums = 0;
        int rows = grid.size();
        if (!rows) return nums;
        int cols = grid[0].size();
        vector<vector<bool>> visit(rows, vector<bool>(cols, false));
        //对所有没有被访问过且对应矩阵中的值为1的坐标进行广搜
        for (int row = 0; row < rows; ++row) {
            for(int col = 0; col < cols; ++col) 
                if (grid[row][col] == '1' && !visit[row][col]) {
                    bfs(grid, row, col, visit);
                    ++nums;
                }
        }
        return nums;
    }

    void bfs(vector<vector<char>>& grid, int row, int col, vector<vector<bool>>& visit) {

        queue<pair<int, int>> q;
        visit[row][col] = true;
        q.push({row, col});
        
        while (!q.empty()) {
            pair<int, int> temp = q.front();
            q.pop();
            //保存当前坐标的下、上、右、左四个方向
            vector<vector<int>> directions = {{1,0}, {-1,0}, {0,1}, {0,-1}};
            for (int i = 0; i < directions.size(); ++i) {
                int new_row = temp.first + directions[i][0];
                int new_col = temp.second + directions[i][1];
                //新坐标在grid中，并且新坐标对应的值为1，并且新坐标没有被访问过，就把新坐标压入队列并打上已访问标记
                if (new_row >= 0 && new_row < grid.size() && new_col >= 0 && new_col < grid[0].size() && grid[new_row][new_col] == '1' && !visit[new_row][new_col]) {
                    q.push({new_row, new_col});
                    visit[new_row][new_col] = true;
                }
            } 

        }

    }
};

复杂度分析

时间复杂度： O(n)，n为网格中元素的总数量。

空间复杂度： O(n)，n为网格中元素的总数量。