题目链接： https://leetcode.cn/problems/subarray-sum-equals-k/

LeetCode 560. 和为 K 的子数组

题目描述

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。

子数组是数组中元素的连续非空序列。

举个例子：

输入：nums = [1,2,3], k = 3
输出：2

思路解析

最简单的解法应该就是暴力枚举所有的子数组并求和，返回和等于k的所有子数组的个数，这种方法的时间复杂度为O(n^2)。下面我来介绍一种基于前缀和的，时间复杂度只有 O(n) 的解法。

因为暴力枚举的过程中会存在大量的重复运算，我们可以尝试把重复的运算保存下来，达到空间换时间的效果。

对于nums = [1, 2, 1, 1]， k = 2。我们观察符合条件的子数组[2]和[1, 1]，对这两个子数组求和可以转成下图的过程。

也就是对子数组[2]求和可以转换成子数组[1, 2]的和减去子数组[1]的和，同样的对子数组[1, 1]求和可以转换成子数组[1, 2, 1, 1]的和减去子数组[1, 2]的和。

上面的子数组[1]，[1,2]，[1, 2, 1, 1]它们均是从原数组[1, 2, 1, 1]第0个元素开始获取的，都是原数组的前缀形式，它们的和就是原数组的前缀和。

我们利用一个哈希表保存原数组所有前缀和跟对应前缀数组的个数。对于nums = [1, 2, 1, 1]， k = 2，对应的哈希表如下。

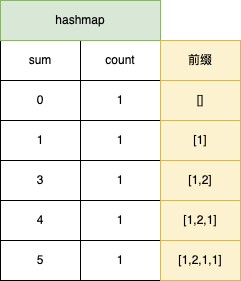
这个哈希表可以预先构建，也可以遍历数组nums时一边寻找符合条件的子数组，一边构建。详细的算法如下：

1. 定义res为符合条件的子数组个数。
2. 遍历数组nums，查找 sum(nums[0],...,nums[i]) - k 是否在哈希表中，如果在那么用res加上哈希表中对应的count值。
3. 把sum(nums[0],...,nums[i])插入到哈希表中，对应的count值加1。
4. 直到遍历完整个数组，返回res。

整个过程一定要注意边界条件的处理，空数组也属于原数组的一个前缀数组，它的前缀和为0。

c++代码

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int res = 0;
        unordered_map<int, int> u_map;
        //数组的前缀和
        int presum = 0;
        u_map[presum] = 1;
        for (int i = 0; i < nums.size(); ++i) {
            presum += nums[i];
            //判断哈希表中是否存在满足条件的前缀和
            if (u_map[presum - k]) {
                res += u_map[presum - k];
            }
            //把当前的前缀和插入到哈希表中
            u_map[presum]++;
        }
        return res;
    }
};

java代码

class Solution {
    public int subarraySum(int[] nums, int k) {
        int res = 0;
        Map<Integer, Integer> u_map = new HashMap<>();
        // 数组的前缀和
        int presum = 0;
        u_map.put(presum, 1);
        
        for (int num : nums) {
            presum += num;
            // 判断哈希表中是否存在满足条件的前缀和
            if (u_map.containsKey(presum - k)) {
                res += u_map.get(presum - k);
            }
            // 把当前的前缀和插入到哈希表中
            u_map.put(presum, u_map.getOrDefault(presum, 0) + 1);
        }
        return res;
    }
}

python代码

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        res = 0
        u_map = defaultdict(int)
        # 数组的前缀和
        presum = 0
        u_map[presum] = 1
        
        for num in nums:
            presum += num
            # 判断哈希表中是否存在满足条件的前缀和
            if u_map[presum - k]:
                res += u_map[presum - k]
            # 把当前的前缀和插入到哈希表中
            u_map[presum] += 1
        
        return res

复杂度分析

时间复杂度： 我们只需要遍历一遍数组，所以时间复杂度为O(n)，n为数组的长度。

空间复杂度： 整个过程会用到一个hash表来保存数组的前缀和，所以空间复杂度为O(n)，n为数组的长度。