 二分查找,你学废了吗
二分查找,你学废了吗
# 二分查找,你学废了吗
# 二分查找介绍
顾名思义二分查找是一种搜索算法,常用在有序数组中查找一个目标值。 二分查找将目标值与数组的中间元素进行比较,来决定是在数组的左半边还是右半边查找目标值,然后在符合条件的半边继续进行二分查找,直到找到目标或符合条件的半边为空。使用二分查找可以在O(logn)时间内完成一个指定元素的搜索。
举个例子,给定一个有序数组arr=[1, 2, 3, 5, 8, 13, 21],让我们找到数组中13所在的位置索引。
最简单的方法就是遍历数组,这样需要将数组中的元素跟目标值比较6次我们才能得到13所在的位置索引。
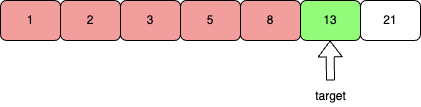
如果使用二分查找,我们首先需要定义两个索引L指向数组第一个元素,R指向数组最后一个元素,即L = 0, R = len(arr) - 1 = 6,我们在[0, 6]这个区间搜索目标值13,然后计算数组中间元素的索引Mid = (L + R) / 2 = 3,此时数组中间元素为arr[3] = 5。
因为5 < 13,所以更新L = Mid + 1 = 4,R = 6保持不变,我们继续在[4, 6]这个区间搜索目标值13。 此时搜索区间的中间元素的索引为 Mid = (L + R) / 2 = 5,因为arr[5] = 13,所以我们找到了目标值13。
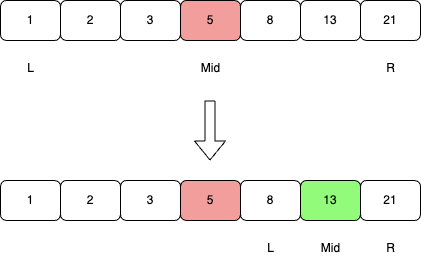
整个搜索过程只将数组中元素跟目标值比较了2次,相比第一种遍历数组(线性搜索),速度提高了3倍,实际上数组中元素越多,二分查找的查找速度优势越明显。
# 二分查找的代码实现
下面介绍两种二分查找的代码实现方式:
- 迭代法
#include <stdio.h>
int binarySearch(int arr[], int L, int R, int target)
{
while (L <= R) {
int Mid = (L + R) / 2;
//如果数组的中间值和目标值相等,就返回中间值的索引
if (arr[Mid] == target)
return Mid;
// 如果目标值比数组的中间值大,那么更新区间的L边界
else if (arr[Mid] < target)
L = Mid + 1;
// 如果目标值比数组的中间值小,那么更新区间的R边界
else
R = Mid - 1;
}
// L>R说明没有找到目标值,返回-1
return -1;
}
// 测试代码
int main(void)
{
int arr[] = {1, 2, 3, 5, 8, 13, 21};
int n = sizeof(arr) / sizeof(arr[0]);
int target = 13;
int result = binarySearch(arr, 0, n - 1, target);
(result == -1) ? printf("目标值不在数组中!\n") :
printf("目标值对应的索引为:%d\n", result);
return 0;
}
代码输出为:
目标值对应的索引为:5
时间复杂度: O(logn),其中n为数组的长度。
空间复杂度: O(1)。
- 递归法
#include <stdio.h>
int binarySearch(int arr[], int L, int R, int target)
{
//没有找到目标值,返回-1
if (L > R)
return -1;
int Mid = (L + R) / 2;
//如果数组的中间值和目标值相等,就结束递归返回中间值的索引
if (arr[Mid] == target)
return Mid;
// 如果目标值比数组的中间值大,那么就继续递归去右边区间[Mid + 1, R]搜索
else if (arr[Mid] < target)
return binarySearch(arr, Mid + 1, R, target);
// 如果目标值比数组的中间值小,那么就继续递归去左边区间[L, Mid - 1]搜索
else
return binarySearch(arr, L, Mid - 1, target);
}
// 测试代码
int main(void)
{
int arr[] = {1, 2, 3, 5, 8, 13, 21};
int n = sizeof(arr) / sizeof(arr[0]);
int target = 13;
int result = binarySearch(arr, 0, n - 1, target);
(result == -1) ? printf("目标值不在数组中!\n") :
printf("目标值对应的索引为:%d\n", result);
return 0;
}
代码输出为:
目标值对应的索引为:5
时间复杂度:O(logn),其中n为数组的长度。
空间复杂度:O(logn),因为递归是通过栈来实现的。
# 使用二分查找需要注意的点
进行二分查找前,数组中的元素必须是有序的。
二分查找实际上也是用的双指针法,双指针指向的应该是数组中的元素,所以在实现二分查找的时候索引
R最好是指向数组的最后一个元素,即R = len(arr) - 1。当然也有些同学习惯把索引R指向数组越界后的一个元素,即R = len(arr)。两种方式在搜索过程中跳出搜索的条件有些差异(L <= R和L < R之间的差异),只要能获得正确答案都可以,不过国内外的算法教科书上还是采用了第一种R = len(arr) - 1。这里只是给大家一个提示,不至于看到其他写法一脸懵,习惯于一种方式就好了,在代码实现的时候可以在纸上模拟一个简单的例子,确保边界条件都考虑到了。要注意边界情况的处理,考虑数组中只有一个元素或两个元素需不需要特殊处理,以及索引L,R的移动条件。
# 二分查找的应用
二分查找可以用作机器学习中算法构建,例如查找模型的最佳超参数。
可用于计算机图形学中的搜索,例如光线追踪或纹理映射的算法。
可以用来查找数据库。
