题目链接： https://leetcode.cn/problems/product-of-array-except-self/

视频题解： https://b23.tv/GEt0p50

LeetCode 238. 除自身以外数组的乘积

题目描述

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums 之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

举个例子：
输入: nums = [1,2,3,4]
输出: [24,12,8,6]

视频讲解

建议大家点击视频跳转到b站除自身以外数组的乘积 (opens new window)观看，体验更佳！

思路解析

题目要求不能使用除法，时间复杂度为O(n)，其中n为nums的长度。

首先引入两个概念，前缀积和后缀积。

前缀积：数组中第i个元素的前缀积为第i个元素之前所有元素的乘积。 后缀积：数组中第i个元素的后缀积为第i个元素之后所有元素的乘积。

我们利用两个跟nums数组长度相同的数组，prefix用来存储nums的前缀积，postfix用来存储nums的后缀积。

prefix[0] = 1
prefix[i] = nums[0] * ... * nums[i-1], 0 < i < n

postfix[n-1] = 1
postfix[i] = nums[i+1]  *... * nums[n-1], 0 <= i < n-1 

数组res用来存储结果。

res[i] = prefix[i] * postfix[i], 0 <= i < n 

对于数组nums = [1,2,3,4]，其计算流程如下：

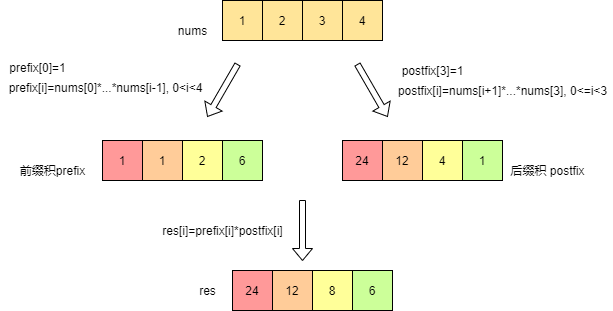
最终结果为res=[24,12,8,6]。

C++代码

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int nums_len = nums.size();
        vector<int> prefix(nums_len, 1);
        vector<int> postfix(nums_len, 1);
        vector<int> res(nums_len, 1);

        //预生成前缀积数组
        prefix[0] = 1;
        for (int i = 1; i < nums_len; ++i) {
            prefix[i] = prefix[i-1] * nums[i-1];
        }
        //预生成后缀积数组
        postfix[nums_len - 1] = 1;
        for (int j = nums_len - 2; j >= 0; --j) {
            postfix[j] = postfix[j+1] * nums[j+1];
        }
        //生成结果
        for (int k = 0; k < nums_len; ++k) {
            res[k] = prefix[k] * postfix[k];
        }
        return res;
    }
};

java代码

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int numsLen = nums.length;
        int[] prefix = new int[numsLen];
        int[] postfix = new int[numsLen];
        int[] res = new int[numsLen];

        // 预生成前缀积数组
        prefix[0] = 1;
        for (int i = 1; i < numsLen; ++i) {
            prefix[i] = prefix[i-1] * nums[i-1];
        }

        // 预生成后缀积数组
        postfix[numsLen - 1] = 1;
        for (int j = numsLen - 2; j >= 0; --j) {
            postfix[j] = postfix[j+1] * nums[j+1];
        }

        // 生成结果
        for (int k = 0; k < numsLen; ++k) {
            res[k] = prefix[k] * postfix[k];
        }

        return res;
    }
}

python代码

class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        nums_len = len(nums)
        prefix = [1] * nums_len
        postfix = [1] * nums_len
        res = [1] * nums_len

        # 预生成前缀积数组
        prefix[0] = 1
        for i in range(1, nums_len):
            prefix[i] = prefix[i-1] * nums[i-1]

        # 预生成后缀积数组
        postfix[nums_len - 1] = 1
        for j in range(nums_len - 2, -1, -1):
            postfix[j] = postfix[j+1] * nums[j+1]

        # 生成结果
        for k in range(nums_len):
            res[k] = prefix[k] * postfix[k]

        return res

代码优化

上面代码我们使用了三个数组prefix、postfix、res，造成了很大浪费。 其实只需要一个res就够了，可以使用一个int型的变量代替数组，中间结果先存在res里面。

prefix[i] = prefix[i-1] * nums[i-1] => prefix = prefix * nums[i-1]

postfix[j] = postfix[j+1] * nums[j+1] => postfix = postfix * nums[j+1]

优化后的C++代码

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int nums_len = nums.size();
        vector<int> res(nums_len, 1);
        int prefix = 1;
        for (int i = 0; i < nums_len; ++i) {
            //正向遍历保存prefix结果到res
            res[i] = prefix;
            prefix = prefix * nums[i];
        }
        int postfix = 1;
        for (int j = nums_len - 1; j >= 0; --j) {
           //逆向遍历 中间结果（前缀积）乘以后缀积
            res[j] = res[j] * postfix;
            postfix = postfix * nums[j];
        }

        return res;
    }
};

优化后的java代码

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int numsLen = nums.length;
        int[] res = new int[numsLen];
        int prefix = 1;
        for (int i = 0; i < numsLen; ++i) {
            // 正向遍历保存prefix结果到res
            res[i] = prefix;
            prefix *= nums[i];
        }
        int postfix = 1;
        for (int j = numsLen - 1; j >= 0; --j) {
            // 逆向遍历 中间结果（前缀积）乘以后缀积
            res[j] *= postfix;
            postfix *= nums[j];
        }
        return res;
    }
}

优化后的python代码

class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        nums_len = len(nums)
        res = [1] * nums_len
        prefix = 1
        for i in range(nums_len):
            # 正向遍历保存prefix结果到res
            res[i] = prefix
            prefix *= nums[i]
        postfix = 1
        for j in range(nums_len - 1, -1, -1):
            # 逆向遍历 中间结果（前缀积）乘以后缀积
            res[j] *= postfix
            postfix *= nums[j]
        return res

复杂度分析

时间复杂度： 只需要遍历一遍nums，故时间复杂度是O(n)，其中n为nums的长度。

空间复杂度： 使用了一个res数组，故空间复杂度是O(n)，其中n为nums的长度。