题目链接： https://leetcode.cn/problems/unique-paths/description/

LeetCode 62. 不同路径

题目描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

举个例子：

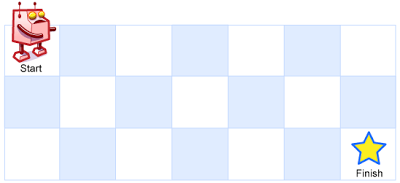
输入：m = 3, n = 7
输出：28

知识回顾

动态规划是一种通过将原问题分解为子问题来求解复杂问题的算法思想。它通常用于求解最优化问题，例如最长公共子序列、背包问题等。动态规划的核心思想是将原问题分解为若干个子问题，通过求解子问题的最优解推导出原问题的最优解。可以通过两点来判断一个问题能不能通过动态规划来解，一是该问题是否存在递归结构，二是对应的子问题能否记忆化。动态规划可以通过带备忘录的自上而下的递归和自下而上的迭代来分别实现。由于递归需要用到栈来实现，一些语言对递归的深度是有限制的，所以自下而上的迭代是动态规划的最佳实现方式。

思路解析

通过分析该问题存在递归结构，并且存在大量子问题可以记忆化保存，所以可以通过动态规划来实现。

本题是经典的二维动态规划问题，需要找到解决动态规划问题的两个突破点：推导出状态转移公式和边界条件处理。

首先定义dp[i][j]为机器人从左上角走到坐标为(i,j)的网格所有的路径数目，i为行，j为列。

根据题意，要走到网格(i,j)，那么只能从网格(i-1,j)出发向下走一步，或者从网格(i,j-1)出发向右走一步。所以我们只要知道从左上角走到(i-1,j)的路径数目dp[i-1][j]和从左上角走到(i,j-1)的路径数目dp[i][j-1]，就可以推算出从左上角走到(i,j)的路径数目dp[i][j] = dp[i-1][j] + dp[i][j-1]。

由于动态规划是自下而上的推导过程，在计算dp[i][j]时，子问题dp[i-1][j]和dp[i][j-1]都是已知结果的。

所以状态转移公式为：

dp[i][j]=dp[i-1][j] + dp[i][j-1], 0 < i < m, 0 < j < n

因为机器人只能往下和往右走，最左边一列和最上面一行的网格都只有1条路，所以边界条件dp[i][0] = 1，dp[0][j] = 1。

对于3 x 7的网格其推导过程如下：

C++代码

  class Solution {
public:
    int uniquePaths(int m, int n) {
        //定义dp并做边界初始化
        vector<vector<int>> dp(m,vector<int>(n,1));
        for(int i = 1;i < m; ++i){
            for(int j = 1; j < n; ++j){
                //状态转移公式
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[m-1][n-1];
    }
};

复杂度分析

时间复杂度： O(mn)，遍历完m x n的网格。

空间复杂度： O(mn)，即dp数组的大小。