 替换后的最长重复字符
替换后的最长重复字符
题目链接: https://leetcode.cn/problems/longest-repeating-character-replacement/
视频题解: https://www.bilibili.com/video/BV1zf421d7Ui/
# LeetCode 424. 替换后的最长重复字符
# 题目描述
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。
在执行上述操作后,返回包含相同字母的最长子字符串的长度。
举个例子:
输入:s = "AABABBA", k = 1
输出:4
解释:
将中间的一个'A'替换为'B',字符串变为 "AABBBBA"。
子串 "BBBB" 有最长重复字母, 答案为 4。
可能存在其他的方法来得到同样的结果。
# 视频讲解
建议大家点击视频跳转到b站替换后的最长重复字符 (opens new window)观看,体验更佳!
# 思路解析
本题是一道比较经典的滑动窗口问题,目标是在字符串s中找到最长的一个窗口,满足最多替换k个字母,窗口就可以变成所有字母都是相同的,这个窗口的长度就是我们要找的答案。
定义left = 0,right = 0来表示窗口的左右边界,res来保存结果,哈希表u_charCount保存当前窗口中所有字母出现的频率。窗口的长度为right - left + 1,窗口中字母出现的最高频率为maxCount。所以right - left + 1 - maxCount就是当前窗口最多要替换的字母数,right - left + 1 - maxCount小于等于k时[left, right]就是我们要找的一个候选窗口。
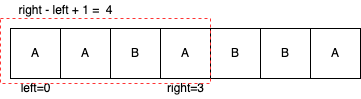
上图中,[left,right]组成的窗口中出现频率最高的字母为A,所以此时maxCount = 3,只需要把B替换成A就可以满足窗口就中所有字母都是相同的。
问题的关键是左右边界如何滑动,窗口滑动策略如下:
right - left + 1 - maxCount <= k时找到以当前right为右边界的候选窗口,更新结果res = max(res, right - left + 1),right向右滑动并更新hash表u_charCount[s[right]]++和当前窗口中字母的最高频率maxCount = max(maxCount, u_charCount[s[right]]),直到right - left + 1 - maxCount > k。right - left + 1 - maxCount > k时未找到以当前right为右边界候选窗口,left向右滑动,更新hash表u_charCount[s[left]]--,直到right - left + 1 - maxCount <= k。
根据上面的策略我们可以获得以s任意位置为右边界(枚举右边界)的所有候选窗口,只需要把其中最长的一个窗口的长度返回即可。
有些同学会有疑问,为啥left向右滑动时只更新了u_charCount,却没有更新maxCount?
这是因为left向右滑动时不会出现比当前res更长的候选窗口,并且此时maxCount不会增大。想获得比当前res更长的候选窗口,必须保证right和maxCount都是相比之前变大的,只有right右滑的时候才会有更长的候选窗口出现,所以left向右滑动时没必要更新maxCount。当然想更新也是可以的,多几行代码,只是没有必要。
# C++代码
class Solution {
public:
int characterReplacement(string s, int k) {
//统计滑动窗口中每个字符出现的次数
unordered_map<char, int> u_charCount;
int res = 0;
int left = 0, right = 0;
//维护滑动窗口中字符出现的最大次数
int maxCount = 0;
int s_len = s.length();
while (right < s_len) {
u_charCount[s[right]] += 1;
maxCount = max(maxCount, u_charCount[s[right]]);
//当最少的操作数大于k,改变左边界,寻找以当前right为右边界的窗口
while (right - left + 1 - maxCount > k) {
u_charCount[s[left]] -= 1;
++left;
}
//更新满足条件的最大窗口
res = max(res, right - left + 1);
++right;
}
return res;
}
};
# java代码
class Solution {
public int characterReplacement(String s, int k) {
// 统计滑动窗口中每个字符出现的次数
Map<Character, Integer> charCount = new HashMap<>();
int res = 0;
int left = 0, right = 0;
// 维护滑动窗口中字符出现的最大次数
int maxCount = 0;
int sLen = s.length();
while (right < sLen) {
charCount.put(s.charAt(right), charCount.getOrDefault(s.charAt(right), 0) + 1);
maxCount = Math.max(maxCount, charCount.get(s.charAt(right)));
// 当最少的操作数大于k,改变左边界,寻找以当前right为右边界的窗口
while (right - left + 1 - maxCount > k) {
charCount.put(s.charAt(left), charCount.get(s.charAt(left)) - 1);
left++;
}
// 更新满足条件的最大窗口
res = Math.max(res, right - left + 1);
right++;
}
return res;
}
}
# python代码
class Solution:
def characterReplacement(self, s: str, k: int) -> int:
# 统计滑动窗口中每个字符出现的次数
char_count = defaultdict(int)
res = 0
left = 0
right = 0
# 维护滑动窗口中字符出现的最大次数
max_count = 0
s_len = len(s)
while right < s_len:
char_count[s[right]] += 1
max_count = max(max_count, char_count[s[right]])
# 当最少的操作数大于k,改变左边界,寻找以当前right为右边界的窗口
while right - left + 1 - max_count > k:
char_count[s[left]] -= 1
left += 1
# 更新满足条件的最大窗口
res = max(res, right - left + 1)
right += 1
return res
# 复杂度分析
时间复杂度: left和right只需要遍历一遍字符串,对u_charCount的操作都是常量时间复杂度,所以整体的时间复杂度是O(n),其中n是字符串的长度。
空间复杂度: 需要使用一个hash表,所以空间复杂度是O(26),即O(1)。
