 课程表
课程表
题目链接: https://leetcode.cn/problems/course-schedule/
# LeetCode 207. 课程表
# 题目描述
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1]表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
举个例子:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
# 知识回顾
在题目讲解之前我们先复习一下涉及到的知识点,以便更好的理解。
首先来复习一下有向图中度的概念,有向图中的度分为入度和出度。
对于一个有向图中的一个顶点,它的入度是指指向该顶点的边的数量,而出度是指从该顶点出发的边的数量。如果一个顶点的入度为0,则称其为源点;如果一个顶点的出度为0,则称其为汇点。
下图中顶点1的入度为0出度为1,顶点4的入度为2出度为0。
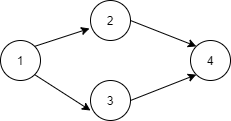
接下来复习一下拓扑排序及其实现。
拓扑排序是一种对有向无环图(DAG)进行排序的算法。在拓扑排序中,对于每个有向边 (u, v),顶点 u 在排序中必须出现在顶点 v 的前面。换句话说,拓扑排序将 DAG 中的所有顶点排成一个线性序列,使得对于所有的有向边 (u, v),顶点 u 在顶点 v 的前面。
拓扑排序实现使用广度优先搜索比较方便,具体算法如下:
- 使用一个队列来存储入度为
0的顶点,然后依次将队列中的顶点出队,并将其所有邻接点的入度减1。如果邻接点的入度减为0,则将其加入队列中。重复这个过程直到队列为空,此时所有顶点都已经被排序。
# 思路解析
# 方法一 拓扑排序
课程之间的关系可以用有向图来表示,能完成课程的依据就是课程组成的有向图中没有环,可以通过拓扑排序来实现。
下图就是一种有环的有向图。
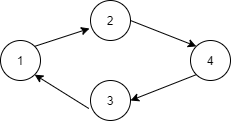
举个例子,对于numCourses = 4,prerequisites = [[0,1],[0,2],[1,3],[2,3]],其课程之间的关系如下图:
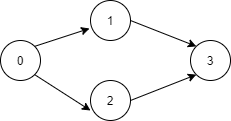
要完成课程0,需要先完成课程1和课程2,要完成课程1和课程2需要先完成课程3。
判断能否完成课程的算法步骤如下,使用了广度优先算法(BFS)。
- 用hash表
preCourse保存每个课程对于的先修课程,用数组ingree保存每个课程组成顶点的入度。
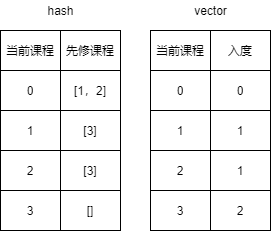
- 所有入度为
0的顶点存入队列并用count计数。 - 当队列中元素不为空,从队列中取出一个元素将此元素对应的所有先修课程的入度减
1,并将入度为0的先修课程存入队列用count计数。 - 直到队列中元素为空,
count==numCourses说明可以完成所有课程。
# C++代码
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
//所有课程的入度
vector<int> ingree(numCourses, 0);
//保存课程和先修课程之间的关系
unordered_map<int, vector<int>> preCourse;
for (int i = 0; i < prerequisites.size(); ++i){
preCourse[prerequisites[i][0]].push_back(prerequisites[i][1]);
ingree[prerequisites[i][1]]++;
}
queue<int> zero_ingree;
int count = 0;
for (int i = 0; i < numCourses; ++i) {
//所有入度为0的课程入队列
if (!ingree[i]) {
zero_ingree.push(i);
++count;
}
}
while(!zero_ingree.empty()) {
int cur_course = zero_ingree.front();
zero_ingree.pop();
for (int i = 0; i < preCourse[cur_course].size(); ++i) {
//当前入度为0的课程对应的先修课程入度减1
--ingree[preCourse[cur_course][i]];
if (!ingree[preCourse[cur_course][i]]) {
//入度为0的课程入队列
zero_ingree.push(preCourse[cur_course][i]);
++count;
}
}
}
//所有课程的入度减为0,说明课程可以修完
if (count == numCourses) return true;
return false;
}
};
# 复杂度分析
时间复杂度: O(m+n),其中m是课程组成有向图的顶点数,n是课程组成有向图的边的个数。
空间复杂度: O(m+n),其中m是课程组成有向图的顶点数,n是课程组成有向图的边的个数。
# 方法二 深度优先搜索(DFS)
还是这个例子,对于numCourses = 4,prerequisites = [[0,1],[0,2],[1,3],[2,3]],其课程之间的关系如下图:

要完成课程0,需要先完成课程1和课程2,要完成课程1和课程2需要先完成课程3。
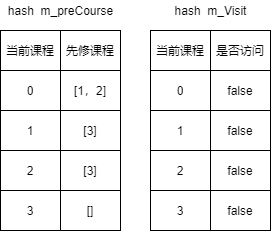
- 用
hash表m_preCourse保存每个课程对于的先修课程,用hash表m_Visit保存每个课程是否被访问。
- 对于课程
cur_course深搜的过程中m_Visit[cur_course]==true说明有向图存在环,直接返回false。 - 对于课程
cur_course,深搜的过程中先修课程列表m_preCourse[cur_course]被置为空说明课程cur_course可以完成。
# C++代码
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
//初始化先修课程列表
for (int i = 0; i < prerequisites.size(); ++i){
m_preCourse[prerequisites[i][0]].push_back(prerequisites[i][1]);
}
//所有课程初始化没有被访问过
for (int i = 0; i < numCourses; ++i) {
m_Visit[i] = false;
}
//所有课程进行dfs
for (int i = 0; i < numCourses; ++i) {
if (!dfs(i)) return false;
}
//所有课程都能完成
return true;
}
bool dfs(int cur_course) {
//cur_course已被访问过,说明存在环
if (m_Visit[cur_course]) {
return false;
}
//cur_course先修课程列表为空说明此课程能完成
if (m_preCourse[cur_course].empty()) {
return true;
}
//保存状态
m_Visit[cur_course] = true;
//对所有的先修课程进行dfs
for(auto& pre_course:m_preCourse[cur_course]) {
if (!dfs(pre_course)) return false;
}
//恢复状态
m_Visit[cur_course] = false;
//所有的先修课程能完成,所以cur_course也能完成,把先修课程列表置为空
m_preCourse[cur_course] = {};
return true;
}
private:
unordered_map<int, vector<int>> m_preCourse;
unordered_map<int, bool> m_Visit;
};
# 复杂度分析
时间复杂度: O(m+n),其中m是课程组成有向图的顶点数,n是课程组成有向图的边的个数。
空间复杂度: O(m+n),其中m是课程组成有向图的顶点数,n是课程组成有向图的边的个数。
