动态规划

动态规划（Dynamic Programming）常用于解决具有重叠子问题和最优子结构的问题。动态规划基于递归的思想，将问题分解成更小的子问题，并利用子问题的解来求解原问题，求解原问题的过程中通过存储子问题的解来避免重复计算，从而提高效率。

通常只需要三步就可以解决所有的动态规划问题。

1. 实现原问题的递归解法。
2. 采用备忘录(数组或哈希表)对递归解法进行优化。
3. 将优化后的算法采用自下而上的迭代重新实现。

下面我们通过著名的斐波那契数列问题来看一下整个过程。

斐波那契数列是一个经典的数学序列，以意大利数学家斐波那契的名字命名。该数列从0和1开始，之后的每一项都是前两项的和。

1. 斐波那契数列的递归解法

观察斐波那契数列的规律，我们可以得到其递推形式：

fib(0) = 0, fib(1) = 1, fib(2) = 1
fib(n) = fib(n-1) + fib(n-2)（n > 2）

当前问题的最优子结构就体现在上面的递推公式中，当前问题的解可以通过子问题的解来构造，即 fib(n) 可以通过 fib(n-1) 和 fib(n-2) 来计算得到。

纯粹的递归解法如下：

def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n-1) + fib(n-2)

下图是fib(5)对应的递归树。

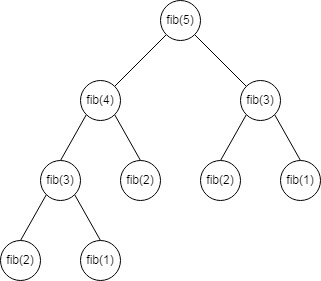
从上面的递归树中我们可以看出，fib(3) , fib(2), fib(1)会被计算多次，从而对于较大的 n 值，会存在大量的重复计算，效率较低，这就是一开始提到的重叠子问题。其时间复杂度为O(2^n)，这是一个指数级的时间复杂度，对于一段代码，这种复杂度简直就是一场灾难。递归涉及到栈的使用，其空间复杂度为O(n)。

2. 利用备忘录对递归进行优化

备忘录法是一种通过保存已经计算过的结果来避免重复计算的方法。由于上面的递归解法中存在大量的重复计算，我们可以利用一个数据结构（通常是数组或哈希表）来存储已经计算过的结果，当需要再次计算时，首先检查备忘录中是否已经有了结果，如果有，则直接返回该结果，否则进行计算。

下面给出了增加备忘录以后的递归代码。

memo = {}
def fib(n):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    else:
        memo[n] = fib(n-1) + fib(n-2)
        return memo[n]

虽然递归看起来是自上而下的层层分解，这里的备忘录实际上是一个隐式的自下而上填表的过程，避免了重复计算，增加备忘录以后的递归解法的时间复杂度为O(n)，大大提高了计算的效率，但需要额外的空间来存储备忘录，这也是常说的用空间换时间。这里的空间复杂度依旧是O(n)。

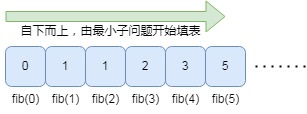
既然带备忘录的递归解法，其本质是隐式的自下而上填表，那我们何不直接通过迭代的方式自下而上的构建问题的解呢？

因此自下而上的迭代实现就应运而生。

3. 使用自下而上的迭代重新实现

自下而上是动态规划的另一种实现方式，与递归相反，它从最小的子问题开始逐步构建解，直到解决原问题，这种方法通常采用迭代实现。

下面是自下而上迭代的代码实现。

def fib(n):
    if n <= 1:
        return n
    dp = [0] * (n+1)
    dp[1] = 1
    for i in range(2, n+1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

分析上面的代码实现，因为数列当前的值只依赖其前面两个数列的值，我们可以进一步优化空间的使用，优化后的代码如下。

def fib(n):
    if n <= 1:
        return n
    pre, cur = 0, 1
    for _ in range(2, n+1):
        pre, cur = cur, pre + cur
    return cur

所以自下而上的迭代甚至可以不需要额外的空间来存储备忘录，更加节省空间，这里的空间复杂度为O(1)。

自下而上的迭代关键在于确定子问题的求解顺序，以确保每个子问题的解都已经计算过。通过自下而上的顺序求解子问题，可以保证每个子问题的解都是基于之前已经求解的子问题，从而确保整体问题的解的正确性，整体的时间复杂度是O(n)。

4. 总结

动态规划是一种重要的问题求解方法，自上而下带备忘录的递归和自下而上的迭代都是动态规划实现方式。

下面是在一维动态规划问题中两种实现方式的时空复杂度对比：

实现方法	时间复杂度	空间复杂度
带备忘录的递归	O(n)	O(n)
迭代	O(n)	能做到O(1)

带备忘录的递归实现可以帮我们更好的理解动态规划，但是有些编程语言，比如python对递归的层级是有限制的，自下而上的迭代相比带备忘录的递归，省去了递归过程中栈的使用，甚至还可以省去备忘录的使用，是实现动态规划问题的最佳选择。

对于所有的动态规划问题，都可以采用上面的步骤，一步一步去实现它的迭代解法。