题目链接： https://leetcode.cn/problems/clone-graph/

LeetCode 133. 克隆图

题目描述

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

知识回顾

深度优先搜索（Depth-First Search，DFS）是一种常见的图遍历算法，它从图的某个顶点开始遍历，沿着一条路径一直走到底，直到不能再走为止，然后回溯到前一个节点，继续沿着另一条路径走到底，直到所有的节点都被访问过为止。

在实现深度优先搜索时，可以使用递归或栈来保存遍历的路径。具体来说，从起始节点开始，将其标记为已访问，然后遍历与该节点相邻的未访问节点，对于每个未访问节点，递归调用深度优先搜索函数，直到所有与起始节点相连的节点都被访问过为止。

思路解析

本题可以采用深度优先（DFS）搜索来解。使用一个hash表存储旧节点和克隆出的新节点之间的一一对应关系。

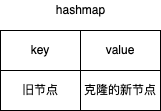
通过hash表即可以方便的获取到已经克隆的新节点，还能知道旧节点是否被克隆过。

dfs算法步骤如下：

1. 如果node已经存在hash表中，直接返回node对应的克隆节点hash[node]。
2. 如果node不在hash表中，对node进行克隆，并将node和克隆节点node_copy存到hash表中，递归地去克隆node的邻居节点，返回node的克隆节点node_copy。

C++代码

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/

class Solution {
public:
    Node* cloneGraph(Node* node) {
        if (!node) return NULL;
        return dfs(node);
    }

    Node* dfs(Node* node) {
       //如果当前节点已经被克隆过直接返回
        if (m_old2new.find(node) != m_old2new.end()) {
            return m_old2new[node];
        }
        //克隆当前节点并存到hash表中
        Node* node_copy = new Node(node->val);
        m_old2new[node] = node_copy;
        for (auto neighbor: node->neighbors) {
            //克隆邻居节点
            node_copy->neighbors.push_back(dfs(neighbor));
        }
        return node_copy;
    }
private:
    //定义一个hash表，unordered_map底层是hash表实现的
    unordered_map<Node*, Node*> m_old2new;
};

复杂度分析

时间复杂度： O(n)，n为原图的节点数。

空间复杂度： O(n)，n为原图的节点数。