题目链接： https://leetcode.cn/problems/set-matrix-zeroes/

LeetCode 73. 矩阵置零

题目描述

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

举个例子：

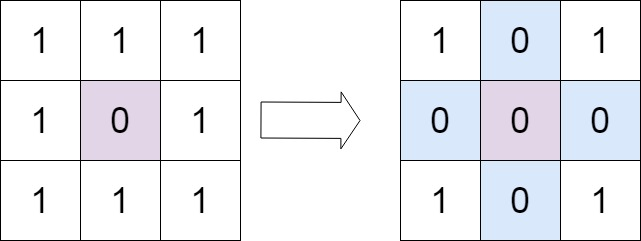
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

思路解析

题目要求使用原地算法，顾名思义，就是使用常量的空间复杂度。我们还是先来看下如何使用额外空间来解，再一步步推导常量空间。

使用两个布尔数组rowsZero、colsZero来保存每一行和每一列是否需要置为0，true代表需要置0。假设matrix = [[1,1,1], [1,0,1], [1,1,1]]，两个数组的情况如下图：

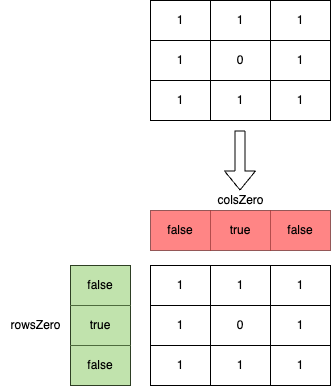
进一步观察矩阵的特征，其实我们可以使用矩阵的第一行来代替colsZero数组，矩阵的第一列(除去第一个元素)外加一个额外的变量(表示第0行是否置0)代替rowsZero数组，值为0表示需要置0。过程如下图所示：

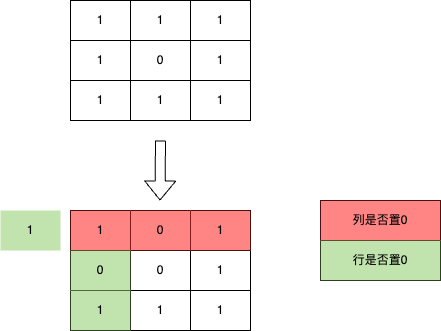
这样只需要使用常量的空间复杂度。

C++代码

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {

        int cols = matrix[0].size(), rows = matrix.size();
        //保存第一行的状态，1表示第一行不置为0
        int zeroRow = 1;
        for (int row = 0; row < rows; ++row) {
            for (int col = 0; col < cols; ++col) {
                if (matrix[row][col] == 0) {
                    //matrix第0行保存第col列是否置为0
                    matrix[0][col] = 0;

                    if (row > 0) {
                        //matrix第0列保存第row行（除第0行）是否置为0
                        matrix[row][0] = 0;
                    } else {
                        //第0行是否置为0单独保存
                        zeroRow = 0;
                    }

                }
            } 
        }
        for (int row = 1; row < rows; ++row) {
            for (int col = 1; col < cols; ++col) {
                if (matrix[row][0] == 0 || matrix[0][col] == 0) {
                    matrix[row][col] = 0;
                } 
            }
        }
        //第0列置为0
        if (matrix[0][0] == 0) {
            for (int row = 1; row < rows; ++row) {
                matrix[row][0] = 0;
            }
        }
        //第0行置为0
        if (zeroRow == 0) {
            for (int col = 0; col < cols; ++col) {
                matrix[0][col] = 0;
            }
        }
    }
};

复杂度分析

时间复杂度： 需要遍历一遍矩阵所以时间复杂度为O(mn)，其中m是矩阵的行数，n是矩阵的列数。

空间复杂度： O(1)。