题目链接： https://leetcode.cn/problems/non-overlapping-intervals/

LeetCode 435. 无重叠区间

题目描述

给定一个区间的集合 intervals ，其中 intervals[i] = [start_i, end_i] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

举个例子：

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

思路解析

首先要明确怎样的区间算是不重叠的，[1, 2]和[2, 3]这两个区间虽然都包含2，但是根据题目的意思他俩是不重叠的。

接下来要制订移除重叠区间的策略。假设区间a=[1, 3]，b=[4, 6]，c=[2, 5]，先对三个区间以区间起点为主键进行排序。如下图，相邻的a、c存在重叠。

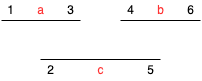
1. 如果移除区间a，那么b和c依旧存在重叠，那么还需移除区间b和c中的一个才能保证剩下的区间不重叠。这个时候总共需要移除2次。
2. 如果移除区间c，a和b不存在重叠。这个时候总共需要移除1次。

总结上面的两种情况，我们发现相邻两个重叠区间中，移除区间终点较大的那个区间可以保证最终移除的区间数是最少的。

C++代码

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        int intervals_len = intervals.size();
        if (intervals_len == 0) 
            return 0;
        //interval的第一个元素作为key排序
        sort(intervals.begin(),intervals.end(),[](const vector<int>& interval1,const vector<int>& interval2){
            return interval1[0] < interval2[0];
        });

        int res = 0;
        int tmpEnd = intervals[0][1];
        for (int i = 1; i < intervals_len; ++i) {
            //没有重叠
            if (intervals[i][0] >= tmpEnd) {
                tmpEnd = intervals[i][1];
            //有重叠
            } else {
                //移除重叠区间[start1，end1]和[start2, end2]中end1、end2值较大的那个区间。
                tmpEnd = min(tmpEnd, intervals[i][1]);
                ++res;
            }
        }
        return res;
    }
};

复杂度分析

时间复杂度： 首先排序的时间复杂度是O(nlogn)，遍历一遍数组intervals需要O(n)，总的时间复杂度是O(nlogn)。其中n为intervals的长度。

空间复杂度： 只需要几个整型变量，故时间复杂度为O(1)。