题目链接： https://leetcode.cn/problems/find-all-anagrams-in-a-string/

LeetCode 438. 找到字符串中所有字母异位词

题目描述

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

举个例子：

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

思路解析

这里我来介绍一种滑动窗口的解法。

定义两个索引left和right，保证字符串s中由区间(left, right]组成窗口的长度始终等于字符串p的长度。

因为单词只包含小写字母，字母总共26个，可以采用两个 长为26的字符串 window_cnt和pchar_cnt，window_cnt用来统计滑动窗口中字符的数量，pchar_cnt用来统计字符串p中字符的数量，如果window_cnt和pchar_cnt相等就说明当前窗口是一个符合条件的窗口，就把当前窗口的起始位置加入到结果中。

字符串的索引和小写字母的对应关系如下图：

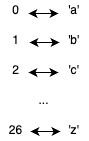
窗口在滑动的过程中，我们只需要更新left和right两个位置的字符在window_cnt中的数量。

c++代码

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        if (p.length() > s.length()) {
            return {};
        }
        vector<int> res;
        //长度为26的字符串统计p中字符的数量
        string pchar_cnt(26, 0);
        //统计滑动窗口中字符的数量
        string window_cnt(26, 0);
        for (int i = 0; i < p.length(); ++i) {
            pchar_cnt[p[i] - 'a'] += 1;
            window_cnt[s[i] - 'a'] += 1;
        }
        if (pchar_cnt == window_cnt)
            res.push_back(0);
        for (int left = 0, right = p.length(); right < s.length(); ++left,++right){
            //窗口滑动的过程中更新window_cnt
            window_cnt[s[left] - 'a'] -= 1;
            window_cnt[s[right] - 'a'] += 1;
            if (pchar_cnt == window_cnt)
                res.push_back(left + 1);
        }
        return res;
    }
};

java代码

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> res = new ArrayList<>();
        
        if (p.length() > s.length()) {
            return res;
        }
        
        int[] pchar_cnt = new int[26];
        int[] window_cnt = new int[26];
        
        // 统计字符串 p 中字符的数量
        for (int i = 0; i < p.length(); i++) {
            pchar_cnt[p.charAt(i) - 'a']++;
        }
        
        // 统计滑动窗口中字符的数量
        for (int i = 0; i < p.length(); i++) {
            window_cnt[s.charAt(i) - 'a']++;
        }
        
        if (Arrays.equals(pchar_cnt, window_cnt)) {
            res.add(0);
        }
        
        int left = 0, right = p.length();
        while (right < s.length()) {
            // 窗口滑动的过程中更新 window_cnt
            window_cnt[s.charAt(left) - 'a']--;
            window_cnt[s.charAt(right) - 'a']++;
            
            if (Arrays.equals(pchar_cnt, window_cnt)) {
                res.add(left + 1);
            }
            
            left++;
            right++;
        }
        
        return res;
    }
}

python代码

class Solution:
    def findAnagrams(self, s: str, p: str) -> List[int]:
        if len(p) > len(s):
            return []
        
        res = []
        pchar_cnt = [0] * 26
        window_cnt = [0] * 26
        
        # 统计字符串 p 中字符的数量
        for char in p:
            pchar_cnt[ord(char) - ord('a')] += 1
        
        # 统计滑动窗口中字符的数量
        for i in range(len(p)):
            window_cnt[ord(s[i]) - ord('a')] += 1
        
        if pchar_cnt == window_cnt:
            res.append(0)
        
        left, right = 0, len(p)
        while right < len(s):
            # 窗口滑动的过程中更新 window_cnt
            window_cnt[ord(s[left]) - ord('a')] -= 1
            window_cnt[ord(s[right]) - ord('a')] += 1
            
            if pchar_cnt == window_cnt:
                res.append(left + 1)
            
            left += 1
            right += 1
        
        return res

复杂度分析

时间复杂度： 我们只需要遍历一遍字符串，所以时间复杂度为O(m+n)，其中m为字符串s的长度，n为字符串p的长度。

空间复杂度： 整个过程需要用到两个长为26的字符串，所以空间复杂度为O(26)，也就是O(1)。