回溯

1. 回溯算法介绍

回溯算法（Backtracking）通过穷举所有可能的解来寻找满足条件解。它的基本思想是从解空间的一个起始节点出发，沿着一条路径搜索解空间，当发现当前路径不可能找到满足条件的解时，就回溯到上一个节点，尝试其他的路径。重复这个过程，直到找到所有可能的解，或者解空间被完全搜索。

回溯算法的特点是它采用了递归的方式，使得代码实现相对简洁。在搜索过程中，可以通过剪枝提前排除那些明显不会得到解的路径，从而减少搜索的总量，提高算法的效率。

回溯算法常用于解决排列组合、地图着色等具有递归特性的问题。

2. 回溯算法的框架模板

回溯算法的基本框架如下，所有回溯相关的问题都可以基于下面的框架稍加改造来实现。

def backtrack(path, choices, result):
    if (valid path):
        result.append(path)
        return

    for (all choices):
        if (valid choice):
            path.append(choice)
            backtrack(path, choices, result)
            path.pop(choice)

3. 回溯算法详解

下面我们通过一个例子来深入的理解一下回溯算法。

假设有三个同学A、B、C，现在要对这三个同学进行排队，请你列出所有可能排队结果。

根据上面的回溯算法框架模板我们可以快速的写出下面的代码。

def backtrack(path, choices, results):
    if len(path) == len(choices):
        # 所有同学都已排队，将当前排列添加到结果列表中
        results.append(path.copy())
        return
    for student in choices:
        if student not in path:
            # 尝试将当前同学加入排队
            path.append(student)
            # 递归继续排列剩余同学
            backtrack(path, choices, results)
            # 回溯，移除当前同学，尝试下一个同学
            path.pop()

对应的测试代码如下。

def all_possible_queues(students):
    results = []  # 存储所有可能的排队方案
    backtrack([], students, results)
    return results

# 假设有三个学生A, B, C
students = ['A', 'B', 'C']
all_queues = all_possible_queues(students)

# 打印所有可能的排队方案
for queue in all_queues:
    print(queue)

对应的递归树如下图，红色的箭头表示做选择，蓝色的箭头表示撤销选择，叶子节点是所有可能的排队顺序。

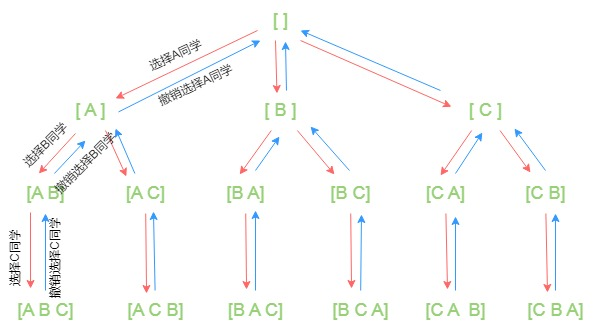
从上图可以看出，要找到所有可能的排队顺序，我们需要遍历递归树所有的节点，这里的时间复杂度是O(3^3)，这是指数级别的时间复杂度！

通常回溯算法中会有一些约束条件，约束条件又分为明确说明的约束条件和隐性的约束条件，所谓隐性的约束条件就是没有明说，但是属于不符常理的一些选择，比如，在旅行商问题中，当前路径的长度不能超过当前最短路径的长度，这就属于一个隐性的约束条件。

我们可以根据约束条件对递归树进行剪枝，从而降低回溯的时间复杂度。

比如，我们给上面的例子增加一个约束条件，A同学不能排在中间，我们给上面的代码加上约束条件。

def backtrack(path, choices, results):
    if len(path) == len(choices):
        # 所有同学都已排队，将当前排列添加到结果列表中
        results.append(path.copy())
        return
    for student in choices:
        if student not in path:
            # 剪枝
            # 如果已经有一个同学排在第一个位置，且下一个同学是A，则跳过
            if len(path) == 1 and student == 'A':
                continue
            # 尝试将当前同学加入排队
            path.append(student)
            # 递归继续排列剩余同学
            backtrack(path, choices, results)
            # 回溯，移除当前同学，尝试下一个同学
            path.pop()

对应的递归树递归树可以根据约束条件剪枝如下图。

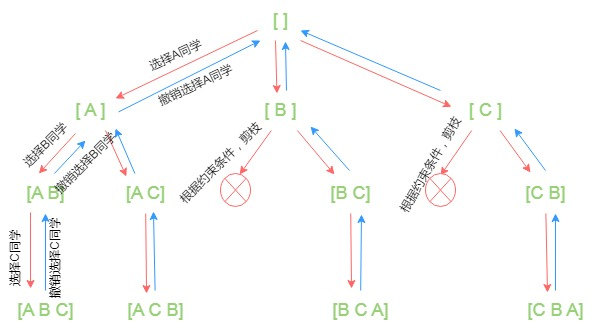
在递归树很庞大的情况下，通过剪枝可以大大缩短搜索的时间。

4. 复杂度分析

对于上面的例子，由于要通过回溯算法去搜索整个递归树，在最坏的情况下，需要进行指数级别的时间复杂度，空间复杂度通常与递归的深度成正比。