题目链接： https://leetcode.cn/problems/spiral-matrix/

LeetCode 54. 螺旋矩阵

题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

举个例子：

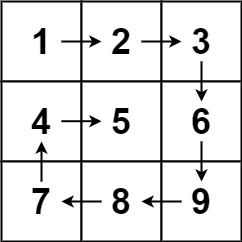
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

思路解析

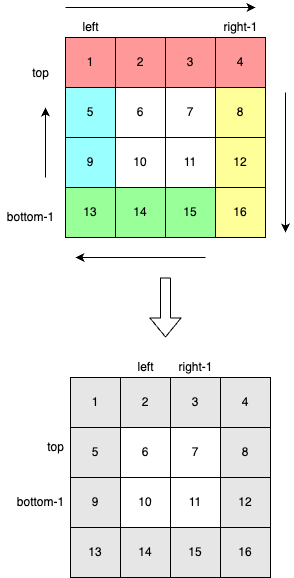
定义四个边界变量left = 0，right = matrix[0].size()， top = 0，bottom = matrix.size()。对于矩阵matrix，其行的范围是[top, bottom)，其列的范围是[left, right)。

算法如下：

1. 先根据题目中的规则遍历矩阵matrix由left，right，top，bottom组成的边界上的元素。
2. 缩小矩阵的边界(++left,--right,++top,--bottom)。如果left >= right 或 top >= bottom结束遍历，否则进入步骤1。

C++代码

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {

        vector<int> res;
        //初始化matrix的四个边界left right top bottom
        int left = 0, right = matrix[0].size(), top = 0, bottom = matrix.size();
        
        while (left < right && top < bottom) {
            //从左到右遍历最上面一行
            for (int i = left; i < right; ++i) {
                res.push_back(matrix[top][i]);
            }
            //最上面一行遍历完修改matrix的top边界
            ++top;
            if (top >= bottom) {
                break;
            }
            //从上到下遍历最右边一列
            for (int j = top; j < bottom; ++j) {
                res.push_back(matrix[j][right - 1]);
            }
            //最右边一列遍历完修改matrix的right边界
            --right;
            //如果已经遍历完matrx就结束，防止matrix只有一行或只有一列，走到下面逻辑重复遍历
            if (left >= right) {
                break;
            }
            //从右到左遍历最下面一行
            for (int k = right - 1; k >= left; --k) {
                res.push_back(matrix[bottom - 1][k]);
            }
            //最下面一行遍历完修改matrix的bottom边界
            --bottom;
            if (top >= bottom) {
                break;
            }
            //从下到上遍历最左边一列
            for (int l = bottom - 1; l >= top; --l) {
                res.push_back(matrix[l][left]);
            }
            ++left;
             if (left >= right) {
                break;
            }
        }
        return res;
    }
};

复杂度分析

时间复杂度： 需要遍历整个矩阵，所以时间复杂度是O(mn)，其中m是矩阵的行数，n是矩阵的列数。

空间复杂度： 需要res来保存结果，所以空间复杂度是O(mn)，其中m是矩阵的行数，n是矩阵的列数。