题目链接： https://leetcode.cn/problems/container-with-most-water/

视频题解： https://www.bilibili.com/video/BV1Dm411k78M/

LeetCode 11.盛最多水的容器

题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明： 你不能倾斜容器。

举个例子：

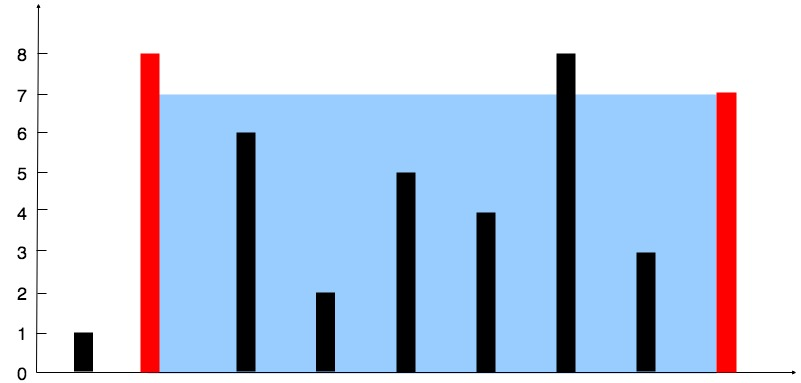
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

视频讲解

建议大家点击视频跳转到b站盛最多水的容器 (opens new window)观看，体验更佳！

思路解析

本题可以使用暴力枚举边界的方式来计算最大值，但是时间复杂度为 O(n²)，oj会判定超时。

下面介绍一个使用双索引的解法。

定义索引L为容器的左边界，索引R为容器的右边界。那么区间[L, R]围成的容器的面积可以表示为area = (R - L) * min(height[L], height[R])，这个面积公式对后续的推导过程很关键。

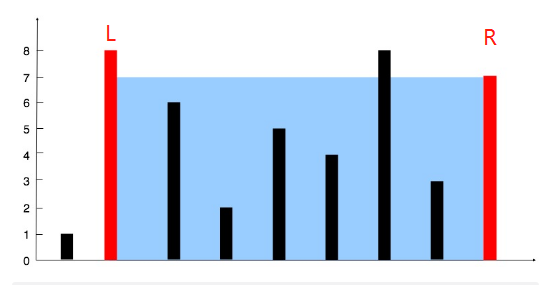
我们知道了面积的计算方式，给定数组height=[1, 8, 6, 2, 5, 4, 8, 3, 7]，初始化索引L = 0，R = height.size - 1。接下来就是要通过移动L，R去寻找区间[L, R]围成的最大的面积。那么L，R要如何移动呢？

假设L = 0，R = 8，height[L] < height[R]。 此时area = (R - L) * min(height[L], height[R]) = (R - L) * height[L] = 8 * 1 = 8。

1. 如果向左移动R，R = R - 1 = 7，area = (R - L) * min(height[L], height[R]) = (R - L) * height[L]。 由于索引R变小了，R - L是一定会变小的，即使height[R]变大，min(height[L], height[R]) = height[L]，短板依旧是height[L]，面积area = (R - L) * height[L] = 7 * 1 = 7会变小。所以移动长板对应的索引R一定会导致面积area变小。

2. 如果向右移动L，L=L+1=1，area = (R - L) * min(height[L], height[R]) =(R - L) * height[R]。 由于索引L变大了，R - L是一定会变小的，但是height[L]变长了，min(height[L], height[R]) = height[R]，短板变成了height[R]，area = (R - L) * height[R] = 7 * 7 = 49变大了。所以移动短板对应的索引L面积area有可能变大。

总结一下上面的过程，移动长板的索引导致区间[L, R]围成的面积area一定会变小，移动短板的索引导致区间[L, R]围成的面积area有可能会变大。我们要找的是最大面积，所以移动长板的索引是没有意义的。这样我们就得到了索引的移动策略：

• 用max_res保存最大当前最大面积，每次移动短板对应的索引，计算area，更新max_res。

C++代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int height_len = height.size();
        int L = 0, R = height_len - 1;
        int max_area = INT_MIN;
        while (L < R) {
           //面积计算公式
            int area = (R - L)*min(height[L], height[R]);
            //更新最大面积
            max_area = max(max_area, area);
            //移动短板对应的索引
            if (height[L] < height[R]) {
                ++L;
            } else {
                --R;
            }
        } 
        return max_area;
    }
};

java代码

class Solution {
    public int maxArea(int[] height) {
        int heightLen = height.length;
        int L = 0, R = heightLen - 1;
        int maxArea = Integer.MIN_VALUE;
        while (L < R) {
            // 面积计算公式
            int area = (R - L) * Math.min(height[L], height[R]);
            // 更新最大面积
            maxArea = Math.max(maxArea, area);
            // 移动短板对应的索引
            if (height[L] < height[R]) {
                L++;
            } else {
                R--;
            }
        }
        return maxArea;
    }
}

python代码

class Solution:
    def maxArea(self, height: List[int]) -> int:
        heightLen = len(height)
        L, R = 0, heightLen - 1
        maxArea = float('-inf')
        while L < R:
            # 面积计算公式
            area = (R - L) * min(height[L], height[R])
            # 更新最大面积
            maxArea = max(maxArea, area)
            # 移动短板对应的索引
            if height[L] < height[R]:
                L += 1
            else:
                R -= 1
        return maxArea

复杂度分析

时间复杂度： 整个过程只遍历了一遍数组height，故时间复杂度为O(n)，其中n为数组height的长度。

空间复杂度： 我们只使用了几个整型的变量，故空间复杂度为O(1)。