 搜索旋转排序数组
搜索旋转排序数组
题目链接: https://leetcode.cn/problems/search-in-rotated-sorted-array/
视频题解: https://www.bilibili.com/video/BV1tz421r7xC/
# LeetCode 33.搜索旋转排序数组
# 题目描述
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
举个例子:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
# 视频讲解
建议大家点击视频跳转到b站搜索旋转排序数组 (opens new window)观看,体验更佳!
# 思路解析
这道题和「LeetCode 153. 寻找旋转排序数组中的最小值」思路基本一致,主要的差异有两点:
- 本题的
target有可能是不存在的。 - 本题的
target是给定的,153中的最小值是未知的。
因为题目要求时间复杂度为 O(log n),所以这道题目的核心思想还是二分查找。初始化索引L = 0,R = nums.size - 1,M = (L + R) / 2,假设目标target = 0。
旋转排序数组有个特点,只需要比较区间两个边界的元素的大小,就可以知道区间是否是单调的。比如,如果nums[L] < nums[M],那么区间[L, M)就是升序的。
我们针对区间[L, M)为升序区间和(M, R]为升序区间两种情况分别讨论。
[L, M)为升序区间。
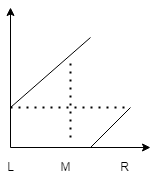
这个时候target如果在升序区间[L, M)范围,后面就只需在升序区间查找R = M - 1。否则L = M + 1。
(M, R]为升序区间。
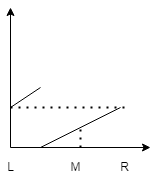
这个时候target如果在升序区间(M, R]范围,后面就只需在升序区间查找L = M + 1。否则R = M - 1。
# C++代码
class Solution {
public:
int search(vector<int>& nums, int target) {
int nums_len = nums.size();
int left = 0, right = nums_len - 1;
while (left <= right) {
int mid = (left + right)/2;
//找到target
if (target == nums[mid]) {
return mid;
}
//[left, mid)有序
if (nums[left] <= nums[mid]) {
//target在左侧有序范围内
if (nums[left] <= target && target < nums[mid]) {
right = mid - 1;
//target在右侧区间
} else {
left = mid + 1;
}
//(mid, right]有序
} else {
//target在右侧有序范围内
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
//target在左侧区间
} else {
right = mid - 1;
}
}
}
return -1;
}
};
# java代码
class Solution {
public int search(int[] nums, int target) {
int numsLen = nums.length;
int left = 0, right = numsLen - 1;
while (left <= right) {
int mid = (left + right) / 2;
//找到target
if (target == nums[mid]) {
return mid;
}
//[left, mid)有序
if (nums[left] <= nums[mid]) {
//target在左侧有序范围内
if (nums[left] <= target && target < nums[mid]) {
right = mid - 1;
//target在右侧区间
} else {
left = mid + 1;
}
//(mid, right]有序
} else {
//target在右侧有序范围内
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
//target在左侧区间
} else {
right = mid - 1;
}
}
}
return -1;
}
}
# python代码
class Solution:
def search(self, nums: List[int], target: int) -> int:
numsLen = len(nums)
left, right = 0, numsLen - 1
while left <= right:
mid = (left + right) // 2
#找到target
if target == nums[mid]:
return mid
#[left, mid)有序
if nums[left] <= nums[mid]:
#target在左侧有序范围内
if nums[left] <= target < nums[mid]:
right = mid - 1
#target在右侧区间
else:
left = mid + 1
#(mid, right]有序
else:
#target在右侧有序范围内
if nums[mid] < target <= nums[right]:
left = mid + 1
#target在左侧区间
else:
right = mid - 1
return -1
# 复杂度分析
时间复杂度: 使用了二分查找,故时间复杂度为 O(log n),其中n为nums的长度。
空间复杂度: 这个过程就使用了有限个整型变量,故空间复杂度为O(1)。
