题目链接： https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

LeetCode 105. 从前序与中序遍历序列构造二叉树

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的前序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

举个例子：

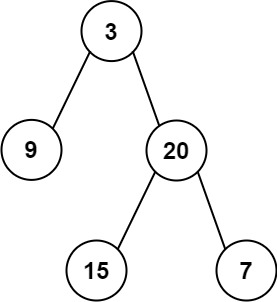
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

知识回顾

二叉树的前序遍历步骤如下：

1. 遍历二叉树的根节点。
2. 遍历二叉树的左子树。
3. 遍历二叉树的右子树。

二叉树的中序遍历步骤如下：

1. 遍历二叉树的左子树。
2. 遍历二叉树的根节点。
3. 遍历二叉树的右子树。

二叉树的前序遍历和中序遍历可以通过递归来实现，当然也可以利用栈通过迭代的方式实现。

思路解析

要想通过序列化的结果构造二叉树，必须要能够从序列化的结果中唯一确定出根节点和左右子树的范围。单纯的通过前序遍历的结果或者中序遍历的结果都无法做到，但是观察前序遍历和中序遍历的特点，把这两种遍历的结果结合在一起就可以唯一确定出根节点和左右子树的范围，从而构造出二叉树。

比如，对于下图中的树。

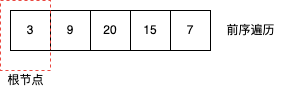
它的前序遍历结果为preorder = [3,9,20,15,7]，根据前序遍历的特点可以确定根节点的值为3。

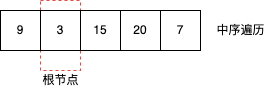
它的中序遍历结果为inorder = [9,3,15,20,7]，从中找到根节点3，那么根节点3左边的区间就是左子树的序列，右边的区间就是右子树的序列。

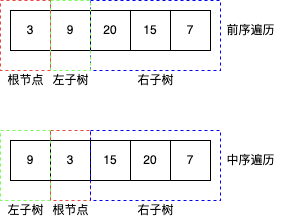
确定了根节点和左右子树序列，通过递归就可以很容易的构造出整棵二叉树。

在中序遍历序列中寻找根节点时，这里使用了一个hash表来保存中序遍历序列中节点值和索引的关系，这种空间换时间的方式可以大大节省寻找根节点时间。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        //保存inorder中节点值和索引之间的一一对应关系
        for (int i = 0; i < inorder.size(); ++i) {
            m_inorderIndex[inorder[i]] = i;
        }
        int preorder_start = 0, preorder_len = preorder.size();
        int inorder_start = 0, inorder_len = inorder.size();
        TreeNode* root = buildTree_help(preorder, inorder, preorder_start, preorder_len, inorder_start, inorder_len);
        return root;
    }

    TreeNode* buildTree_help(vector<int>& preorder, vector<int>& inorder, int preorder_start, int preorder_len, int inorder_start, int inorder_len) {
        //递归结束的条件
        if (preorder_len <= 0 || inorder_len <= 0) {
            return NULL;
        }
        TreeNode* node = new TreeNode(preorder[preorder_start]);
        int node_in_inorder = m_inorderIndex[preorder[preorder_start]];
        //递归生成左子树
        node->left = buildTree_help(preorder, inorder, preorder_start + 1, node_in_inorder - inorder_start, inorder_start, node_in_inorder - inorder_start);
        //递归生成右子树
        node->right = buildTree_help(preorder, inorder, preorder_start + 1 + node_in_inorder - inorder_start, inorder_len - node_in_inorder + inorder_start - 1, node_in_inorder + 1, inorder_len - node_in_inorder + inorder_start - 1);
        return node;
    }
 
private:
    unordered_map<int, int> m_inorderIndex;
};

复杂度分析

时间复杂度： 需要遍历整棵二叉树，所以时间复杂度跟二叉树的总节点数相关。

空间复杂度： 整个过程会用到递归和一个hash表来存储二叉树中序遍历数组中节点和索引的关系，递归用到的函数栈的最大长度跟二叉树的高度相关，hash表的大小和二叉树的总节点数相关，所以总的空间复杂度跟二叉树的总节点数相关。