题目链接： https://leetcode.cn/problems/binary-tree-level-order-traversal/

LeetCode 102. 二叉树的层序遍历

题目描述

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

举个例子：

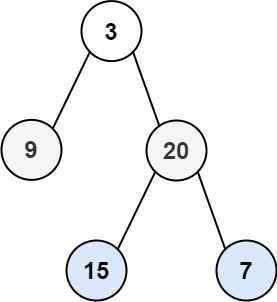
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

知识回顾

广度优先搜索（BFS） 是一种图形搜索算法，它的基本思想是从一个顶点出发，先访问它的所有邻接顶点，然后再按照同样的方式访问这些邻接顶点的未访问邻接顶点，直到图中所有顶点都被访问。广度优先搜索算法通常使用队列来存储待访问的顶点，并使用一个数组或者集合来记录已访问的顶点。

思路解析

二叉树作为一种特殊的图，广度优先搜索（BFS）同样适用于二叉树的遍历，广搜的特点就是一层一层的遍历，很符合题目中按层序遍历的要求。因为广搜一般会使用一个队列来保存待访问的节点，节点进入队列的顺序又决定了每一层的节点访问时的顺序。对于二叉树如果左孩子先入队那么每一层的访问顺序是从左到右，如果右孩子先入队那么每一层的访问顺序是从右到左。

下面就以题目描述中给的例子来模拟下整个层序遍历的过程，为了更好的理解广搜在层序遍历中的应用，同学们最好在纸上自己模拟一遍加深理解。

1. 根节点首先入队。

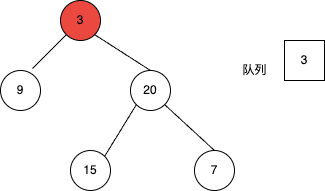
2. 访问队列中的二叉树的第一层节点，并将第一层节点的左孩子和右孩子依次入队。第一层节点访问完，第二层的节点自左向右已经全部入队。

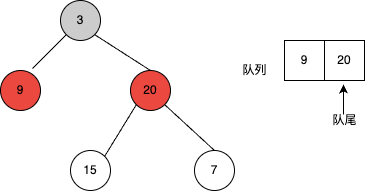
3. 访问队列中的二叉树的第二层节点，并将第二层节点的左孩子和右孩子依次入队。第二层节点访问完，第三层的节点自左向右已经全部入队。

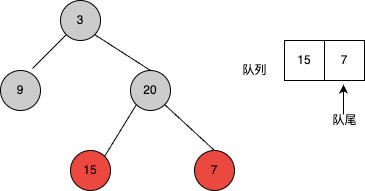
4. 直到队列为空，返回的顺序为[[3], [9, 20], [15, 7]]。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        queue<TreeNode*> q;
        if (root)
        q.push(root);
        while (!q.empty()) {
            //队列中元素的个数
            int q_len = q.size();
            vector<int> tmp_vec;
            //从队列中取出q_len在同一层的元素
            for (int i = 0; i < q_len; ++i ) {
                TreeNode* node = q.front();
                q.pop();
                tmp_vec.push_back(node->val);

                //把左右孩子放入队列中，左孩子先入队列
                if (node->left)
                    q.push(node->left);
                if (node->right)
                    q.push(node->right); 
             }
            if (q_len > 0) {
                res.push_back(tmp_vec);
            }
        }
        return res;
    }
};

复杂度分析

时间复杂度： 需要遍历整棵树，所以时间复杂度和树的总节点数相关。

空间复杂度： 需要利用一个队列，队列的长度和树的总节点数相关，所以空间复杂度也是和树的总节点数相关。