题目链接： https://leetcode.cn/problems/kth-smallest-element-in-a-bst/

LeetCode 230. 二叉搜索树中第K小的元素

题目描述

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

举个例子：

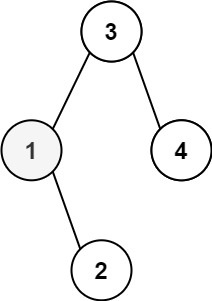
输入：root = [3,1,4,null,2], k = 1
输出：1

知识回顾

二叉树的中序遍历步骤如下：

1. 遍历二叉树的左子树。
2. 遍历二叉树的根节点。
3. 遍历二叉树的右子树。

思路解析

对二叉搜索树进行中序遍历，其节点值组成的序列是单调递增的。

比如对于下图的二叉搜索树进行中序遍历，得到一个单调递增的序列[1,2,3]。

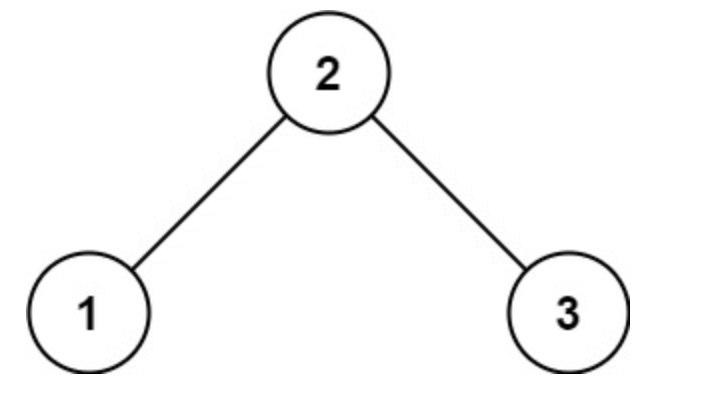
这里要得到二叉搜索树第k小的元素，最简单的方法就是对二叉搜索树进行中序遍历，遍历过程中把访问到的节点的值存到一个数组vals里，最终只需要返回数组vals的第k个元素即可。

上面的方法需要遍历整棵二叉搜索树，很多时候我们是不需要遍历完整棵树的，这里可以在中序遍历二叉树的时候采用非递归的实现方式，在访问到第k个元素的时候就结束遍历。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        int cnt = 0;
        stack<TreeNode*> s;
        TreeNode* cur_node = root;
        while (cur_node || !s.empty()) {
            //左孩子入栈
            while (cur_node) {
                s.push(cur_node);
                cur_node = cur_node->left;
            }
            //访问栈顶的节点
            cur_node = s.top();
            s.pop();
            ++cnt;
            if (cnt == k) {
                return cur_node->val;
            }
            //右孩子入栈
            cur_node = cur_node->right;
        }
        return cur_node->val;
    }
};

复杂度分析

时间复杂度： 需要遍历前k个节点，但是如果二叉树的高度hight比k大，需要先把左孩子一直压栈，所以时间复杂度跟二叉树的高度hight和k值均相关。

空间复杂度： 整个过程会用到一个栈，栈的长度最长为树的高度，所以空间复杂度跟树的高度相关。