题目链接： https://leetcode.cn/problems/binary-tree-maximum-path-sum/

LeetCode 124. 二叉树中的最大路径和

题目描述

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

举个例子：

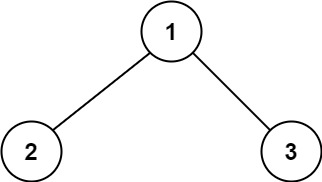
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

思路解析

首先定义变量 lmax表示root的左子树中能与root节点组成合法路径的节点组合的最大和。对于下图中的root节点，绿色的节点[1,3]就是其左子树中能与root组成合法路径的节点组合，此时lmax = 4。同样定义 rmax表示root右子树中能与root节点组成合法路径的节点组合的最大和。定义 res保存二叉树中合法路径最大和。

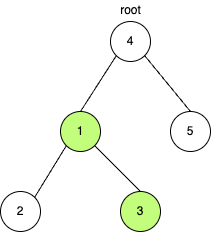
本题可以使用递归，难点在于不能简单的把二叉树的最大路径和分解为左子树的最大路径和与右子树的最大路径和的组合。我们通过递归来获取左子树中能与root组成合法路径的节点组合最大和lmax与右子树中能与root组成合法路径的节点组合最大和rmax，并在递归函数中更新res。

下面讨论三种更新res的最基本情况。

1. 所有节点的值均为正数。

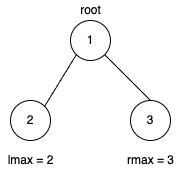
此时合法路径最大和res = lmax + rmax + root->val。

2. 孩子节点中存在值为负数。

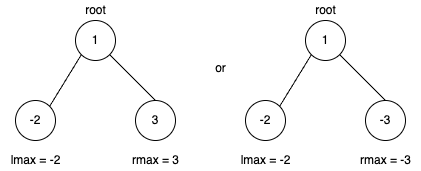
此时为负数值的节点不能包含到路径中，否则路径的和会变小。所以这个时候需要对上面的公式进行改造一下res = max(lmax, 0) + max(rmax, 0) + root->val。

3. 根节点值为负数。

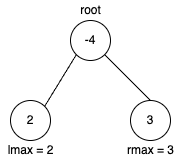
这时根节点可能会导致新的路径和比左子树的最大路径和或右子树的最大路径和小，所以需要进一步对上面的公式进行改造res = max(res, max(lmax, 0) + max(rmax, 0) + root->val)。

通过上面的讨论我们得到了最大路径和的推导公式。那么lmax和rmax怎么更新呢？

如下图，root'的lmax = max(lmax, rmax) + root->val。

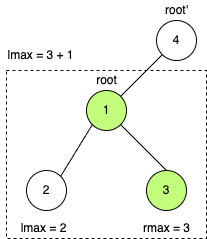
同样地可以去计算rmax的值。

根据上面的讨论我们需要在递归函数中更新res、lmax、rmax，详细代码如下。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxPathSum(TreeNode* root) {
        int res = root->val;
        dfs(root, res);
        return res;
    }

    int dfs(TreeNode* root, int& res) {
        if (!root) {
            return 0;
        }
        int lmax = dfs(root->left, res);
        lmax = max(lmax, 0);
        int rmax = dfs(root->right, res);
        rmax = max(rmax, 0);
        res = max(res, root->val + lmax + rmax);
        return root->val + max(lmax, rmax);
    } 
 };

复杂度分析

时间复杂度： 因为需要遍历所有的节点，所以时间复杂度和二叉树节点的总数相关。

空间复杂度： 因为用到了递归，需要用到栈来保存递归函数，栈的最大长度为二叉树的高度，所以空间复杂度和二叉树的高度相关。