 二叉树的序列化与反序列化
二叉树的序列化与反序列化
题目链接: https://leetcode.cn/problems/serialize-and-deserialize-binary-tree/
# LeetCode 297. 二叉树的序列化与反序列化
# 题目描述
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
提示: 输入输出格式与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
举个例子:
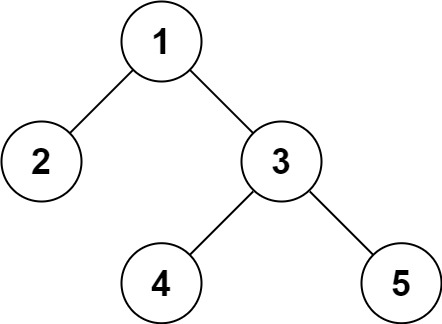
输入:root = [1,2,3,null,null,4,5]
输出:[1,2,3,null,null,4,5]
# 思路解析
题目要求将二叉树序列化以后还能根据序列化的结果反序列化出二叉树,这里能够反序列化的关键是能在序列化以后的结果中唯一的区分根节点和左右子树的范围。任何一种单独的二叉树遍历方式都是无法反序列化的,但是我们可以对遍历的结果进行改造,增加一些特殊标记,使得可以从序列化结果中唯一的区分根节点和左右子树。
比如,对于root = [1,2,3,null,null,4,5]这棵树,如下图。
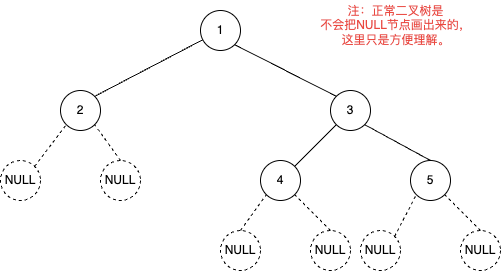
它的前序遍历结果为"1,2,3,4,5",对于这个结果,如果没有任何额外信息我们只能判断出根节点是1,左子树和右子树无法唯一的确定。如果对前序遍历稍加改造,NULL节点也保存起来,那么结果就变成"1,2,N,N,3,4,N,N,5,N,N",其中'N'表示NULL点。结合二叉树的特点和改造后前序遍历的结果,很容易唯一的确定根节点和左右子树范围。
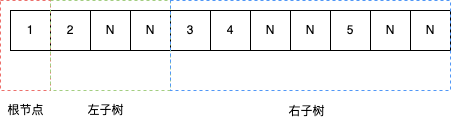
根据上面的讨论,本题的序列化方案如下:
- 采用前序遍历。
NULL节点也保存下来。
反序列化实现使用递归,因为二叉树的构造可以分解成左子树的构造和右子树的构造两个独立的子问题,边界条件即递归结束的条件为遇到N字符就返回。
当然使用改造的前序遍历进行序列化只是众多方案中的一种,任何可以唯一的确定根节点和左右子树范围的序列化方案都可以解决本题。
# C++代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string res;
serialize_help(root, res);
return res;
}
void serialize_help(TreeNode* root, string& res) {
if (!root) {
if (res.length() == 0) {
res += "N";
return;
} else {
res += ",N";
return;
}
}
if (res.length() == 0) {
res += to_string(root->val);
} else {
res += ",";
res += to_string(root->val);
}
//递归序列化左子树
serialize_help(root->left, res);
//递归序列化右子树
serialize_help(root->right, res);
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
vector<string> nodes;
string tmp;
for (int i = 0; i < data.length(); ++i) {
if (data[i] == ',') {
nodes.push_back(tmp);
//清空tmp
tmp.clear();
} else {
tmp += data[i];
}
}
//最后一个node进入vector
if (tmp.length()) {
nodes.push_back(tmp);
}
int index = 0;
TreeNode* root = deserialize_help(nodes, index);
return root;
}
TreeNode* deserialize_help(vector<string>& nodes, int& index) {
if (nodes[index] == "N") {
++index;
return NULL;
}
TreeNode* node = new TreeNode(stoi(nodes[index]));
++index;
node->left = deserialize_help(nodes, index);
node->right = deserialize_help(nodes, index);
return node;
}
};
// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));
# 复杂度分析
时间复杂度: 需要遍历整棵树,所以时间复杂度跟二叉树的总节点数相关。
空间复杂度: 序列化和反序列化的过程中用到了递归,递归需要用到函数调用栈,栈的最大长度跟二叉树的高度相关。
