题目链接： https://leetcode.cn/problems/maximum-depth-of-binary-tree/

LeetCode 104. 二叉树的最大深度

题目描述

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

举个例子：

给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

思路解析

方法一 递归法

递归的关键是将问题分解成独立的子问题。

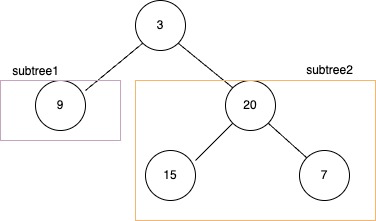
如上图所示，以root为根节点树的高度 可以分解成 以root->left为根节点树的高度depth1 和 以root->right为根节点树的高度depth2 中的较大值加一，即max{depth1, depth2} + 1。

递归是函数一层一层调用的过程，函数调用实际上是一个入栈出栈的过程，这里的栈就是函数调用栈，你可以用gdb调试一个程序通过bt命令来查看函数调用栈。这里的递归函数是maxDepth，它的入参是树的根节点，返回值是树的高度。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        
        if (!root) {
            return 0;
        }

        return 1 + max(maxDepth(root->left), maxDepth(root->right)); 

    }
};

复杂度分析

时间复杂度： 递归需要遍历整棵树所以时间复杂度和树的总节点数相关。

空间复杂度： 递归需要利用函数调用栈来保存函数，其栈的最大长度和树的高度相关。

方法二 广度优先(BFS)

广度优先搜索（BFS） 是一种图形搜索算法，它的基本思想是从一个顶点出发，先访问它的所有邻接顶点，然后再按照同样的方式访问这些邻接顶点的未访问邻接顶点，直到图中所有顶点都被访问。广度优先搜索算法通常使用队列来存储待访问的顶点，并使用一个数组或者集合来记录已访问的顶点。

广度优先搜索同样可以应用到树的搜索中，具体流程参考下面的代码。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        
        if (!root) {
            return 0;
        }

        int depth = 0;
        queue<pair<TreeNode*,int>> q;
        q.push({root,1});
        while (!q.empty()) {
            auto temp = q.front();
            q.pop();
            depth = max(depth, temp.second);
            if (temp.first->left) {
                q.push({temp.first->left, temp.second + 1});
            }
            if (temp.first->right) {
                q.push({temp.first->right, temp.second + 1});
            }
        } 
        return depth;
    }
};

复杂度分析

时间复杂度： 广度优先需要遍历整棵树所以时间复杂度和树的总节点数相关。

空间复杂度： 广度优先利用队列来保存树的节点，其空间复杂度也是和树的最后一层的节点数相关。

方法三 深度优先(DFS)

深度优先搜索（Depth-First Search，DFS）是一种常见的图遍历算法，它从图的某个顶点开始遍历，沿着一条路径一直走到底，直到不能再走为止，然后回溯到前一个节点，继续沿着另一条路径走到底，直到所有的节点都被访问过为止。

在实现深度优先搜索时，可以使用递归或栈来保存遍历的路径。具体来说，从起始节点开始，将其标记为已访问，然后遍历与该节点相邻的未访问节点，对于每个未访问节点，递归调用深度优先搜索函数，直到所有与起始节点相连的节点都被访问过为止。

深度优先搜索同样可以应用到树的搜索中，具体流程参考下面的代码。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        
        if (!root) {
            return 0;
        }

        int depth = 0;
        stack<pair<TreeNode*,int>> s;
        s.push({root,1});
        while (!s.empty()) {
            auto temp = s.top();
            s.pop();
            depth = max(depth, temp.second);
            if (temp.first->left) {
                s.push({temp.first->left, temp.second + 1});
            }
            if (temp.first->right) {
                s.push({temp.first->right, temp.second + 1});
            }
        } 
        return depth;
    }
};

复杂度分析

时间复杂度： 深度优先需要遍历整棵树所以时间复杂度和树的总节点数相关。

空间复杂度： 深度优先利用栈来保存树的节点，其空间复杂度也是和树的高度相关。