题目链接： https://leetcode.cn/problems/validate-binary-search-tree/

LeetCode 98. 验证二叉搜索树

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

举个例子：

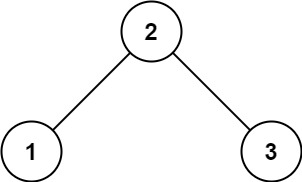
输入：root = [2,1,3]
输出：true

知识回顾

二叉树的中序遍历步骤如下：

1. 遍历二叉树的左子树。
2. 遍历二叉树的根节点。
3. 遍历二叉树的右子树。

中序遍历通过递归实现起来比较方便。

思路解析

对二叉搜索树进行中序遍历，其节点值组成的序列是单调递增的。

比如对于下图的二叉搜索树进行中序遍历，得到一个单调递增的序列[1,2,3]。

验证一棵二叉树是否是二叉搜索树，我们可以直接对这棵树进行中序遍历，把遍历得到的节点值存到数组vals里，如果vals是单调递增的那么这棵树就是二叉搜索树。 这里用到一个数组vals，我们在判断数组是否单调会用到两个索引，pre，cur = pre + 1，遍历整个数组如果vals[pre] < vals[cur]恒成立，说明数组是单调的。

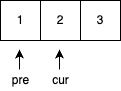
我们可以对上面的流程进一步优化，不需要把节点的值存的数组里，定义一个全局变量pre_val存储中序遍历过程中上一个访问的值，可以一边遍历，一边比较当前访问的值和上一个访问的值pre_val的大小。只需要对二叉树的中序遍历稍加改造就可以实现。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        long long pre_val = LONG_MIN;
        return isValidBST_help(root, pre_val);
    }
    bool isValidBST_help(TreeNode* root, long long& pre_val) {
        if (!root) return true;
        //左子树不满足二叉搜索树
        if (!isValidBST_help(root->left, pre_val)) return false;
        //根节点和上一个被访问的节点的值比较
        if (root->val <= pre_val) return false; 
        //中序遍历更新pre_val
        pre_val = root->val;
        //右子树不满足二叉搜索树
        if (!isValidBST_help(root->right, pre_val)) return false;
        //整棵树满足二叉搜索树
        return true;
    }
};

复杂度分析

时间复杂度： 需要遍历整棵数，所以时间复杂度跟二叉树的总节点数相关。

空间复杂度： 验证的过程使用了递归，递归需要用到函数调用栈，函数栈的最大长度跟二叉树的高度相关。